题目内容
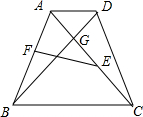
等腰梯形ABCD中,AD∥BC,∠ABC=60゜,且AC⊥AB,AB=20,则梯形ABCD的周长为( )
| A.100 | B.50
| C.40+20
| D.60
|
∵AC⊥AB,
∴∠CAB=90°,
∵∠B=60∴∠ACB=30°,
∵AB=20
∴BC=2AB=40,
∵四边形ABCD是等腰梯形,AD∥BC,∠B=60°,AB=20,
∴DC=AB=20,∠DCB=∠B=60°,
过A作AE∥DC交BC于E,
∵AD∥BC,
∴四边形AECD是平行四边形,
∴AE=DC=20=AB,AD=CE
∵∠B=60°,
∴△ABE是等边三角形,
∴BE=AB=20,
∴AD=CE=40-20=20,
∴等腰梯形ABCD的周长是AB+BC+CD+AD=20+40+20+20=100,
故选A.


练习册系列答案
相关题目

 EC、BF、CF.
EC、BF、CF.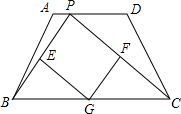

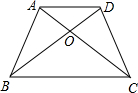
 于AB,AC于点E,点F,下列结论正确的是( )
于AB,AC于点E,点F,下列结论正确的是( )