题目内容
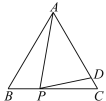
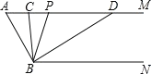
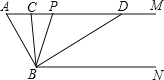
【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上的动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于点C、D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB∶∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
【答案】(1)50°;(2)不变,∠APB:∠ADB=2:1,理由详见解析;(3)∠ABC=25°.
【解析】
(1)先根据平行线的性质求出∠ABN,然后再根据角平分线的定义即可求出∠CBD;
(2)先根据平行线的性质可得∠APB=∠PBN、∠ADB=∠DBN,然后再由角平分线的定义即可发现规律;
(3)由平行线的性质可得∠ACB=∠CBN=50°+∠DBN,再结合条件可得到∠DBN=∠ABC,且∠ABC+∠DBN=60°,即可求解.
解:(1)∵AM∥BN,
∴∠ABN+∠A=180°,
又∵∠A=80°,
∴∠ABN=180°-80°=100°,
∴∠ABP+∠PBN=100°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=100°,
∴∠CBD=∠CBP+∠DBP=50°;
(2)不变,∠APB:∠ADB=2:1.
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB:∠ADB=2:1;
(3)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
由(1)可知∠ABN=100°,∠CBD=50°,
∴∠ABC+∠DBN=50°,
∴∠ABC=25°.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案