题目内容
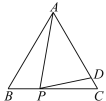
【题目】如图,△ABC为等边三角形,点P为边BC上一点,在AC上取一点D,使AD=AP.
(1)若∠APD=80°,求∠DPC的度数;
(2)若∠APD=α,求∠BAP(用含α的式子表示).
【答案】(1)∠DPC=20°;(2)∠BAP=2α-120°.
【解析】
(1)在△APD中,求得∠PAD的度数,进而求得∠APC的度数,进而即可求解;
(2)由(1)解题思路和三角形的内角和定理即可求出∠BAP的度数.
(1)在△APD中,AP=AD,
∴∠APD=∠ADP=80°
∴∠PAD=180°-80°-80°=20°
∴∠BAP=60°-20°=40°
∴∠APC=∠B+∠BAP=60°+40°=100°
∴∠DPC=∠APC-∠APD=100°-80°=20°.
(2)∵在△APD中,AP=AD,
∴∠APD=∠ADP=α°
∴∠PAD=180°-α°-α°=180°-2α°
∴∠BAP=60°-(180°-2α°)=(2α-120)°.

练习册系列答案
相关题目