题目内容
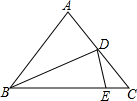
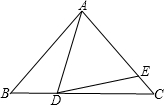
如图，△ABC中，AB=AC，∠BAD=25°，且AD=AE，则∠EDC=（ ）
| A．25° | B．10° | C．15° | D．12.5° |
设∠EDC=x．则∠AED=∠ADE=x+∠C（外角定理）；
∵AD=AE（已知），
∴∠ADE=∠AED（等边对等角）；
又∵∠EAD+∠AED+∠ADE=180°（三角形内角和定理），
∴∠EAD=180°-2∠AED=180°-2（x+∠C）；
而AB=AC（已知），∴∠B=∠C（等边对等角），
又∵∠B+∠C+∠BAC=180°（三角形内角和定理），
∴∠BAC=180°-2∠C
∵∠BAC=∠BAD+∠EAD
∴180°-2∠C=25°+180°-2（x+∠C）
∴∠EDC=
=12.5°．
故选D．
∵AD=AE（已知），
∴∠ADE=∠AED（等边对等角）；
又∵∠EAD+∠AED+∠ADE=180°（三角形内角和定理），
∴∠EAD=180°-2∠AED=180°-2（x+∠C）；
而AB=AC（已知），∴∠B=∠C（等边对等角），
又∵∠B+∠C+∠BAC=180°（三角形内角和定理），
∴∠BAC=180°-2∠C
∵∠BAC=∠BAD+∠EAD
∴180°-2∠C=25°+180°-2（x+∠C）
∴∠EDC=
| 25° |
| 2 |
故选D．
练习册系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
