题目内容
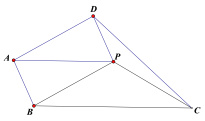
【题目】如图,在△ABC中,AD为∠BAC的平分线,点E在BC的延长线上,且∠EAC=∠B,以DE为直径的半圆交AD于点F,交AE于点M.
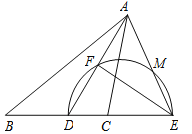
(1)判断AF与DF的数量关系,并说明理由.
(2)只用无刻度的直尺画出△ADE的边DE上的高AH(不要求写做法,保留作图痕迹) .
(3)若EF=8,DF=6,求DH的长.
【答案】(1)AF=DF;(2)答案见试题解析;(3)![]() .
.
【解析】
(1)AF=DF,理由是:求AE=DE,由等腰三角形的性质求出即可;
(2)由锐角三角形的三条高交于一点画出即可;
(3)证△ADH∽△EDF,得出比例式,代入求出即可.
(1)AF=DF,理由如下:
∵AD平分∠BAC,∴∠BAD=∠CAD.又∵∠B=∠CAE,∴∠BAD+∠B=∠CAD+∠CAE.即∠ADE=∠DAE,∴AE=DE,∵DE是直径,∴EF⊥AD,∴AF=DF;
(2)如图:连接DM,DM交EF于G,作射线AG交DE于H,此时AH是高.
(3)在△EFD中,EF=8,DF=6,由勾股定理得,DE=AE=10,∵AH是DE边上的高,∴∠AHD=90°,∵∠EFD=90°,∴∠AHD=∠EFD,∵∠ADH=∠EDF,∴△ADH∽△EDF,∴DH:DF=AD:DE,∴DH:6=12:10,解得DH=![]() .
.

练习册系列答案
相关题目