题目内容
【题目】如图1,在![]() 中,AB=AC,∠ABC =
中,AB=AC,∠ABC =![]() ,D是BC边上一点,以AD为边作
,D是BC边上一点,以AD为边作![]() ,使AE=AD,
,使AE=AD,![]() +
+![]() =180°.
=180°.
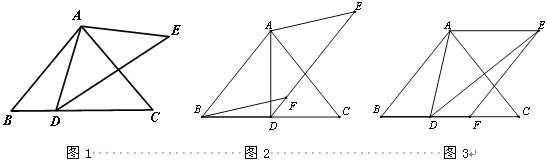
(1)直接写出∠ADE的度数(用含![]() 的式子表示);
的式子表示);
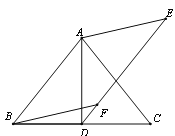
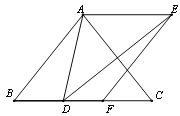
(2)以AB,AE为边作平行四边形ABFE,
①如图2,若点F恰好落在DE上,求证:BD=CD;
②如图3,若点F恰好落在BC上,求证:BD=CF.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题(1)由在△ABC中,AB=AC,∠ABC=α,可求得∠BAC=180°-2α,又由AE=AD,∠DAE+∠BAC=180°,可求得∠DAE=2α,继而求得∠ADE的度数;
(2)①由四边形ABFE是平行四边形,易得∠EDC=∠ABC=α,则可得∠ADC=∠ADE+∠EDC=90°,证得AD⊥BC,又由AB=AC,根据三线合一的性质,即可证得结论;
②由在△ABC中,AB=AC,∠ABC=α,可得∠B=∠C=α,四边形ABFE是平行四边形,可得AE∥BF,AE=BF.即可证得:∠EAC=∠C=α,又由(1)可证得AD=CD,又由AD=AE=BF,证得结论.
试题解析:(1)∠ADE =![]() .
.
(2)①证明:∵四边形ABFE是平行四边形,
∴AB∥EF.
∴![]() .
.
由(1)知,∠ADE =![]() ,
,
∴![]() .
.
∴AD⊥BC.
∵AB=AC,
∴BD=CD.
②证明:
∵AB=AC,∠ABC =![]() ,
,
∴![]() .
.
∵四边形ABFE是平行四边形,
∴AE∥BF,AE=BF.
∴![]() .
.
由(1)知,![]() ,
,
∴![]() .
.
∴![]() .
.
∴AD=CD.
∵AD=AE=BF,
∴BF=CD.
∴BD=CF.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】养成良好的早锻炼习惯,对学生的学习和生活都非常有益,某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间x(分钟)进行了调查.现把调查结果分成A、B、C、D四组,如表所示,同时,将调查结果绘制成下面两幅不完整的统计图.
分组 | A | B | C | D |
x(分钟)的范围 | 0≤x<10 | 10≤x<20 | 20≤x<30 | 30≤x<40 |
请你根据以上提供的信息,解答下列问题:

(1)补全频数分布直方图;
(2)所抽取的七年级学生早锻炼时间的中位数落在______组内(填“A”或“B”或“C”或“D”);
(3)已知该校七年级共有1200名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.(早锻炼:指学生在早晨7:00~7:40之间的锻炼)




