题目内容
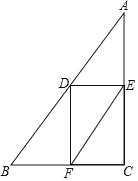
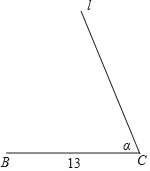
【题目】如图，线段BC长为13，以C为顶点，CB为一边的∠α满足cosα＝
．锐角△ABC的顶点A落在∠α的另一边上，且满足sinA＝
．求△ABC的高BD及AB边的长，并结合你的计算过程画出高BD及AB边．（图中提供的单位长度供补全图形使用）
【答案】BD=12,AB=15,补图详见解析.
【解析】
先利用直角作出BD，再用勾股定理求出BD，再用锐角三角函数求出AB，AD，即可得出结论．
解：如图，作BD⊥l于点D，
在Rt△CBD中，∠CDB＝90°，BC＝13，
∴cosC＝cosα＝
，
∴CD＝BCcosC＝13×＝5，BD＝
＝12，
在Rt△ABD中，BD＝12，sinA＝
，
∴tanA＝
，
∴AB＝
＝15，AD＝
＝9，
作图，以点D为圆心，9为半径作弧与射线l交于点A，连接AB，
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
