题目内容
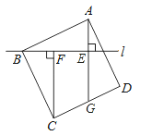
【题目】如图,在△ABC中,∠C=90°,点D是边AB上的动点,过点D作DE∥BC交AC于E,过E作EF∥AB交BC于F,连结DF.
(1)若点D是AB的中点,证明:四边形DFEA是平行四边形;
(2)若AC=8,BC=6,直接写出当△DEF为直角三角形时AD的长.
【答案】(1)见解析;(2)AD的值为5或![]() .
.
【解析】
(1)先证明DF∥AE,EF∥AD即可;
(2)分两种情形分别求解即可解决问题;
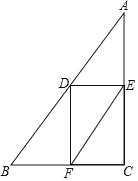
(1)证明:∵AD=DB,DE∥BC,
∴AE=EC,
∵EF∥AB,
∴BF=CF,∵AD=DB,
∴DF∥AC,∵EF∥AB,
∴四边形DFEA是平行四边形.
(2)情形1:当点D是AB的中点,由(1)可知:DE∥BC,DF∥EC,
∴四边形DECF是平行四边形,
∵∠ECF=90°,
∴四边形DECF是矩形,
∴∠EDF=90°,△DEF是直角三角形,此时AD=![]() AB=
AB=![]() ×
×![]() =5.
=5.
情形2:如图,当∠DFE=90°时,设AD=x.
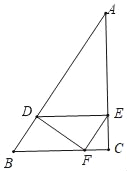
则AE=![]() x.BD=10﹣x,EC=8﹣
x.BD=10﹣x,EC=8﹣![]() x,BF=
x,BF=![]() (10﹣x),CF=
(10﹣x),CF=![]() (8﹣
(8﹣![]() x),
x),
∵BF+CF=6,
∴![]() (10﹣x)+
(10﹣x)+![]() (8﹣
(8﹣![]() x)=6
x)=6
∴x=![]() ,
,
综上所述,AD的值为5或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目