题目内容
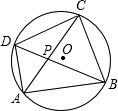 如图,点A、B、C、D在⊙O上,AC、BD相交于点P,图中有几对相似三角形?
如图,点A、B、C、D在⊙O上,AC、BD相交于点P,图中有几对相似三角形?
- A.2对
- B.3对
- C.4对
- D.5对
A
分析:根据相似三角形的判定定理;由两组对应角相等的两个三角形相似,即可找出相似三角形个数.
解答:在△APD和△BPC中,∠APD=∠BPC(对顶角),
∠PCB=∠PDA(同弧所对的圆周角相等),
由此可判断△APD∽△BPC,
同理可得△APB∽△CPD,所以有2对相似三角形.
故选A.
点评:此题主要考查学生利用:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似,这一定理来判定相似三角形的,此题还要熟练掌握圆周角定理.这是证明题的基础,要求学生一定要牢记这些知识点,为以后的学习打下坚实的基础.
分析:根据相似三角形的判定定理;由两组对应角相等的两个三角形相似,即可找出相似三角形个数.
解答:在△APD和△BPC中,∠APD=∠BPC(对顶角),
∠PCB=∠PDA(同弧所对的圆周角相等),
由此可判断△APD∽△BPC,
同理可得△APB∽△CPD,所以有2对相似三角形.
故选A.
点评:此题主要考查学生利用:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似,这一定理来判定相似三角形的,此题还要熟练掌握圆周角定理.这是证明题的基础,要求学生一定要牢记这些知识点,为以后的学习打下坚实的基础.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
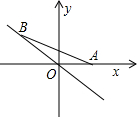 如图,点A的坐标为(2
如图,点A的坐标为(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|
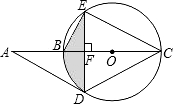 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°.
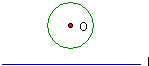 12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是
12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是