题目内容
如图所示,四边形ABCD的对角线AC,BD相交于点O,△ABC≌△BAD.

求证:(1)OA=OB;(2)AB∥CD.
见解析
【解析】分析:(1)要证OA=OB,由等角对等边知需证∠CAB=∠DBA,由已知△ABC≌△BAD即可证得.(2)要证AB∥CD,根据平行线的性质需证∠CAB=∠ACD,由已知和(1)可证得∠OCD=∠ODC,又因为∠AOB=∠COD,所以可证得∠CAB=∠ACD,即AB∥CD获证.
证明:(1)因为 △ABC≌△BAD,所以 ∠CAB=∠DBA,所以 OA=OB.
(2)因为 △ABC≌△BAD,所以 AC=BD.
又因为 OA=OB,所以 AC-OA=BD-OB,
即OC=OD,所以 ∠OCD=∠ODC.
因为 ∠AOB=∠COD,∠CAB=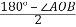 ,∠ACD=
,∠ACD=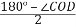 ,
,
所以 ∠CAB=∠ACD,所以 AB∥CD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




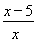
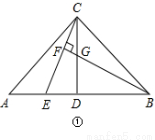


 ,高DF= .
,高DF= .