Question

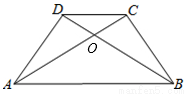
已知：在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．

（1）直线BF垂直于直线CE，交CE于点F，交CD于点G（如图①），求证：AE=CG；

（2）直线AH垂直于直线CE，交CE的延长线于点H，交CD的延长线于点M（如图②），找出图中与BE相等的线段，并证明．

 

 

Answer 1

见解析

【解析】⑴证明：设∠ACE=∠1,因为直线BF垂直于CE，交CE于点F,所以∠CFB=90°，

所以∠ECB+∠CBF=90°.

又因为∠1+∠ECB=90°，所以∠1=∠CBF .

因为AC=BC, ∠ACB=90°，所以∠A=∠CBA=45°.

又因为点D是AB的中点，所以∠DCB=45°.

因为∠1=∠CBF，∠DCB=∠A，AC=BC，所以△CAE≌△BCG，所以AE=CG.

(2)【解析】
CM=BE.证明如下：因为∠ACB=90°,所以∠ACH +∠BCF=90°.

因为 CH⊥AM，即∠CHA=90°,所以 ∠ACH +∠CAH=90°,所以∠BCF=∠CAH.

因为 CD为等腰直角三角形斜边上的中线,所以 CD=AD.所以∠ACD=45°.

在△CAM与△BCE中,CA=BC,∠CAH =∠BCF, ∠ACM =∠CBE,

所以 △CAM ≌△BCE,所以CM=BE.