题目内容
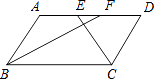
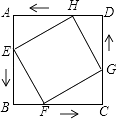
【题目】如图1所示,边长为a的正方形中有一个边长为b的小正方形,图2是由图1中阴影部分拼成的一个长方形,设图1中阴影部分面积为S1,图2中阴影部分面积为S2.
(1)请直接用含a,b的代数式表示S1=______,S2=_____;
(2)写出利用图形的面积关系所揭示的公式:_______;
(3)利用这个公式说明216﹣1既能被15整除,又能被17整除.

【答案】(1)a2﹣b2;(a+b)(a﹣b);(2)a2﹣b2=(a+b)(a﹣b);(3)证明见解析.
【解析】
(1)图1用大正方形的面积去掉小正方形的面积,图2用长方形的面积计算公式;
(2)因为两个图形的阴影部分面积相等,可以根据第(1)问列出等式;
(3)利用所得到的平方差公式分解因式后进行说明.
(1)图1用大正方形的边长为a,小正方形的边长为b,故阴影部分面积为a2﹣b2,图2用长方形的长为(a+b),宽为(a﹣b),故阴影部分面积为(a+b)(a﹣b);
(2)观察图1和图2中阴影部分面积是相等的,故a2﹣b2=(a+b)(a﹣b);
(3)216﹣1=(28﹣1)(28+1)=(24﹣1)(24+1)(28+1)=15×17×(28+1)
因为28+1是整数,故216﹣1既能被15整除,又能被17整除.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目