题目内容
【题目】如图,已知△ABC中,AB=AC,BE平分∠ABC交AC于E,若∠A=90°,那么BC、BA、AE三者之间有何关系?并加以证明.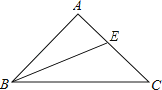
【答案】解:BC、BA、AE三者之间的关系:BC=BA+AE,理由如下:
过E作ED⊥BC交BC于点D,∵BE平分∠ABC,BA⊥CA,∴AE=DE,∠EDC=∠A=∠BDE=90°,∵在Rt△BAE和Rt△BDE中,BE=BE,AE=DE,∴Rt△BAE≌Rt△BDE(HL),
∴BA=BD,∵AB=AC,∠A=90°∴∠C=45°,∴∠CED=45°=∠C,∴DE=CD,∵AE=DE,
∴AE=CD=DE,∴BC=BD+DC=BA+AE.
【解析】先根据直角三角形的判定Rt△BAE≌Rt△BDE,再根据角平分线的性质进行等量代换.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.

练习册系列答案
相关题目