题目内容
(2008•长宁区二模)如图,AB为⊙O的直径,点C在AB的延长线上,点D在⊙O上,且AD=CD,如果tanC=
,BC=1.求AD长?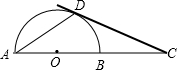
| ||
| 3 |

分析:连接OD,先由AD=CD可知∠A=∠C,再根据tanC=
可求出∠C的度数,由三角形内角和定理可求出∠ADC的度数,再由OA=OD可求出∠CDO的度数,进而可判断出△ODC是直角三角形,再根据锐角直角三角形的性质可求出OD及CD的长,即可得出AD的长.
| ||
| 3 |
解答: 解:连接OD.
解:连接OD.
∵AD=CD,
∴∠A=∠C,
∵tanC=
,
∴∠A=∠C=30°,
∴∠ADC=180°-∠C-∠A=180°-30°-30°=120°,
∵OA=OD,
∴∠A=∠ADO=30°,
∴∠CDO=∠ADC-∠ADO=120°-30°=90°,
在Rt△DOC中,
∵∠C=30°,
∴OD=
OC,
∵OD=OB,
∴OD=DB=BC=1,
∴OC=2,
∴CD=OC•cos30°=2×
=
,
∴AD=CD=
.
 解:连接OD.
解:连接OD.∵AD=CD,
∴∠A=∠C,
∵tanC=
| ||
| 3 |
∴∠A=∠C=30°,
∴∠ADC=180°-∠C-∠A=180°-30°-30°=120°,
∵OA=OD,
∴∠A=∠ADO=30°,
∴∠CDO=∠ADC-∠ADO=120°-30°=90°,
在Rt△DOC中,
∵∠C=30°,
∴OD=
| 1 |
| 2 |
∵OD=OB,
∴OD=DB=BC=1,
∴OC=2,
∴CD=OC•cos30°=2×
| ||
| 2 |
| 3 |
∴AD=CD=
| 3 |
点评:本题考查的是圆周角定理、等腰三角形的判定与性质、直角三角形的判定与性质、三角形内角和定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 (2008•长宁区二模)如图,实数a、b在数轴上对应的点分别为A、B,化简
(2008•长宁区二模)如图,实数a、b在数轴上对应的点分别为A、B,化简