Question

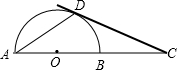
（2008•长宁区二模）如图，在△ABC中，∠C=90°，点O为AB中点，以O为坐标原点，x轴与AC平行，y轴与CB平行，建立直角坐标系，AC与y轴交于点M，BC与x轴交于点N．将一把三角尺的直角顶点放在坐标原点O处，绕点O旋转三角尺，三角尺的两直角边分别交射线CA、射线BC于点P、Q．
（1）证明：△OMP∽△ONQ；
（2）若∠A=60°，AB=4．设点P的横坐标为x，PQ长为L．当点P在边AC上运动时，求L与x的函数关系式及定义域；
（3）若∠A=60°，AB=4．当△PQC的面积为

3

2

时，试求CP的长．

Answer 1

分析：（1）根据∠OMC=∠ONQ=90°，∠MOP=∠NOQ，即可得出△OMP∽△ONQ；
（2）根据OM=AOsin60°=

3

，求出P纵坐标，设P（x，-

3

），PM=|x|，根据△BON≌△OAM，得出AM=ON，AM=AOcos60°=1，由相似得

ON

OM

=

OQ

OP

=

1

3

，OP=

3

OQ，得出OP²和OQ²，即可求出L²，从而得出A和C点的坐标，最后求出L与x的函数关系式及定义域；
（3）根据PQ=L，得出CP=1-x和

ON

QN

，再根据PM=|x|，QN=

|x|

3

，得出CQ的值，最后根据S=

1

2

CQ•CP，得出x的值，即可求出CP的长；

解答：（1）证明：∵∠OMC=∠ONQ=90°，
∵∠MOP=90°-∠PON，∠NOQ=90°-∠PON
∴∠MOP=∠NOQ
∴△OMP∽△ONQ；

（2）解：AO=

AB

2

=2，
OM=AOsin60°=

3

，
∴P纵坐标是-

3

，
P（x，-

3

），PM=|x|，
∵O是AB中点，
∴△BON≌△OAM，
∴AM=ON，
AM=AOcos60°=1，
由上面相似得

ON

OM

=

OQ

OP

=

1

3

，
∴OP=

3

OQ，
OP²=OM²+MP²=3+x²
OQ²=

OP2

3 2

=

x 2+3

3

，
L²=

4x2+12

3

，
L=

2 3 ( x2 +3)

3

，
CM=ON=AM=1
∴A（-1，-

3

），C（1，-

3

），
∴-1≤x≤1，

（3）解：PQ=L=

2 3 ( x2 +3)

3

，
AC=2，
则CM=1，
∴CP=1-x，
∵

OQ

OP

=

1

3

，
∴

ON

QN

=

1

3

，
PM=|x|，QN=

3

ON=

|x|

3

，
CN=OM=

3

，
∴CQ=QN+CN=

3

+

|x|

3

，
∴S=

1

2

CQ•CP=

1

2

（

3

+

|x|

3

）（1-x）=

3

2

，
x₁=0，x₂=1-

3

，
∵-1＜x＜1，
∴x=1-

3

，
CP=1-x=1-（1-

3

）=

3

．

点评：此题考查了相似三角形的判定与性质；解题的关键是根据相似三角形的性质求出线段的长度，在计算时要注意x的取值范围．