题目内容
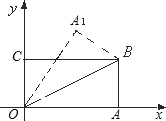 如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知OA=8,OC=4,则点A1的坐标为( )
如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知OA=8,OC=4,则点A1的坐标为( )| A、(4.8,6.4) | B、(4,6) | C、(5.4,5.8) | D、(5,6) |
分析:设出A1点的坐标,先根据翻折变换的性质得出△A1BD的面积,作A1E⊥x轴于E,交DE于F,根据BC∥x轴可知A1E⊥BC,再由(1)中BD的值及三角形的面积公式可求出A1F的长,B点坐标,用待定是法求出过O、D两点的一次函数的解析式,把A1点的坐代入函数解析式即可.
解答:解:∵BC∥AO,
∴∠BOA=∠OBC,
根据翻折不变性得,
∠A1OB=∠BOA,
∴∠OBC=∠A1OB,
∴DO=DB.
设DO=DB=xcm,
则CD=(8-x)cm,
又∵OC=4,
∴(8-x)2+42=x2,
解得x=5.
∴BD=5,
∴S△BDO=
×5×4=10;
设A1(a,4+b),作A1E⊥x轴于E,交DE于F,如下图所示:
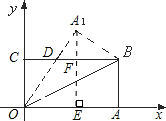 ∵BC∥x轴,
∵BC∥x轴,
∴A1E⊥BC,
∵S△OAB=
OA•AB=
×8×4=16,S△BDO=10.
∴S△A1BD=
BD•A1F=
×5A1F=6,
解得A1F=
,
∴A点的纵坐标为
,
∵BD=5,B(8,4)
∴D点坐标为(3,4),
∴过OC两点直线解析式为y=
x,
把A点的坐标(a,
)代入得,
=
a,
解得a=
,
∴A点的坐标为(
,
).
故选A.
∴∠BOA=∠OBC,
根据翻折不变性得,
∠A1OB=∠BOA,
∴∠OBC=∠A1OB,
∴DO=DB.
设DO=DB=xcm,
则CD=(8-x)cm,
又∵OC=4,
∴(8-x)2+42=x2,
解得x=5.
∴BD=5,
∴S△BDO=
| 1 |
| 2 |
设A1(a,4+b),作A1E⊥x轴于E,交DE于F,如下图所示:
 ∵BC∥x轴,
∵BC∥x轴,∴A1E⊥BC,
∵S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△A1BD=
| 1 |
| 2 |
| 1 |
| 2 |
解得A1F=
| 12 |
| 5 |
∴A点的纵坐标为
| 32 |
| 5 |
∵BD=5,B(8,4)
∴D点坐标为(3,4),
∴过OC两点直线解析式为y=
| 4 |
| 3 |
把A点的坐标(a,
| 32 |
| 5 |
| 32 |
| 5 |
| 4 |
| 3 |
解得a=
| 24 |
| 5 |
∴A点的坐标为(
| 24 |
| 5 |
| 32 |
| 5 |
故选A.
点评:本题考查的是图形的翻折变换、用待定系数法求正比例函数的解析式、直角三角形的性质,熟知以上知识是解答此题的关键.

练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: