题目内容
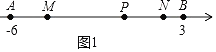
【题目】如图,数轴上点A,B表示的有理数分别为﹣6,3,点P是射线AB上一个动点(不与点A,B重合).M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.
![]()
(1)若点P表示的有理数是0,那么MN的长为 ;若点P表示的有理数是6,那么MN的长为 .
(2)点P在射线AB上运动(不与点A,B重合)的过程中,MN的长是否发生改变?若不改变,请写出求MN的长的过程;若改变,请说明理由.
【答案】(1)6;6;(2)MN的长不会发生改变,理由见解析
【解析】
(1)若点P表示的有理数是0,则AP=6,BP=3,根据题意先求出MP和NP,从而求出MN;若点P表示的有理数是6,则AP=12,BP=3,根据题意先求出MP和NP,从而求出MN;
(2)设点P表示的数是a(a>﹣6且a≠3),然后根据点P的位置分类讨论:当﹣6<a<3时,AP=a+6,BP=3﹣a,根据题意先求出MP和NP,从而求出MN;当a>3时,AP=a+6,BP=a﹣3,根据题意先求出MP和NP,从而求出MN.
解:(1)若点P表示的有理数是0(如图1),则AP=6,BP=3.
∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.
∴MP=![]() AP=4,NP=
AP=4,NP=![]() BP=2,
BP=2,
∴MN=MP+NP=6;
若点P表示的有理数是6(如图2),则AP=12,BP=3.

∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.
∴MP=![]() AP=8,NP=
AP=8,NP=![]() BP=2,
BP=2,
∴MN=MP﹣NP=6.
故答案为:6;6.
(2)MN的长不会发生改变,理由如下:
设点P表示的数是a(a>﹣6且a≠3).
当﹣6<a<3时(如图1),AP=a+6,BP=3﹣a.
∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.
∴MP=![]() AP=
AP=![]() (a+6),NP=
(a+6),NP=![]() BP=
BP=![]() (3﹣a),
(3﹣a),
∴MN=MP+NP=6;
当a>3时(如图2),AP=a+6,BP=a﹣3.
∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.
∴MP=![]() AP=
AP=![]() (a+6),NP=
(a+6),NP=![]() BP=
BP=![]() (a﹣3),
(a﹣3),
∴MN=MP﹣NP=6.
综上所述:点P在射线AB上运动(不与点A,B重合)的过程中,MN的长为定值6.

 愉快的寒假南京出版社系列答案
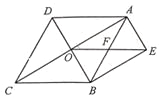
愉快的寒假南京出版社系列答案【题目】如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=10,AC=16,求菱形ABCD的面积.
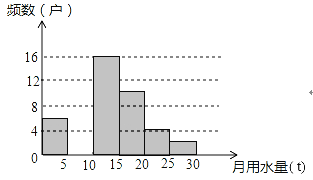
【题目】八年级(1)班同学为了解某小区家庭月均用水情况,随机调査了该小区部分家庭,并将调查数据整理成如下两幅不完整的统计图表:
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | m | 0.24 |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | n |
25<x≤30 | 2 | 0.04 |
请根据以上信息,解答以下问题:
(1)直接写出频数分布表中的m、n的值并把频数直方图补充完整;
(2)求出该班调查的家庭总户数是多少?
(3)求该小区用水量不超过15的家庭的频率.