题目内容
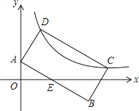
【题目】如图,在平面直角坐标系![]() 中,直线y=kx+3与
中,直线y=kx+3与![]() 轴、
轴、![]() 轴分别相交于点A、B,并与抛物线
轴分别相交于点A、B,并与抛物线![]() 的对称轴交于点
的对称轴交于点![]() ,抛物线的顶点是点
,抛物线的顶点是点![]() .
.
(1)求k和b的值;
(2)点G是![]() 轴上一点,且以点
轴上一点,且以点![]() 、C、
、C、![]() 为顶点的三角形与△
为顶点的三角形与△![]() 相似,求点G的坐标;
相似,求点G的坐标;
(3)在抛物线上是否存在点E:它关于直线AB的对称点F恰好在y轴上.如果存在,直接写出点E的坐标,如果不存在,试说明理由.
【答案】(1)k=-![]() ,b=1;(2) (0,1)和
,b=1;(2) (0,1)和![]()
【解析】分析:(1) 由直线![]() 经过点
经过点![]() ,可得
,可得![]() .由抛物线
.由抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,可得
,可得![]() ,进而得到A、B、D的坐标,然后分两种情况讨论即可;
,进而得到A、B、D的坐标,然后分两种情况讨论即可;
(3)设E(a,![]() ),E关于直线AB的对称点E′为(0,b),EE′与AB的交点为P.则EE′⊥AB,P为EE′的中点,列方程组,求解即可得到a的值,进而得到答案.
),E关于直线AB的对称点E′为(0,b),EE′与AB的交点为P.则EE′⊥AB,P为EE′的中点,列方程组,求解即可得到a的值,进而得到答案.
详解:(1) 由直线![]() 经过点
经过点![]() ,可得
,可得![]() .
.
由抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,可得
,可得![]() .
.
∵直线![]() 与x轴、y轴分别相交于点
与x轴、y轴分别相交于点![]() 、
、![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
∵抛物线的顶点是点![]() ,∴点
,∴点![]() 的坐标是
的坐标是![]() .
.
∵点![]() 是
是![]() 轴上一点,∴设点
轴上一点,∴设点![]() 的坐标是
的坐标是![]() .
.
∵△BCG与△BCD相似,又由题意知,![]() ,
,
∴△BCG与△![]() 相似有两种可能情况:
相似有两种可能情况:
①如果![]() ,那么
,那么![]() ,解得
,解得![]() ,∴点
,∴点![]() 的坐标是
的坐标是![]() .
.
②如果![]() ,那么
,那么![]() ,解得
,解得![]() ,∴点
,∴点![]() 的坐标是
的坐标是![]() .
.
综上所述:符合要求的点![]() 有两个,其坐标分别是
有两个,其坐标分别是![]() 和
和![]() .
.
(3)设E(a,![]() ),E关于直线AB的对称点E′为(0,b),EE′与AB的交点为P,则EE′⊥AB,P为EE′的中点,∴
),E关于直线AB的对称点E′为(0,b),EE′与AB的交点为P,则EE′⊥AB,P为EE′的中点,∴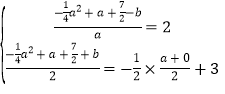 ,整理得:
,整理得:![]() ,∴(a-2)(a+1)=0,解得:a=-1或a=2.
,∴(a-2)(a+1)=0,解得:a=-1或a=2.
当a=-1时,![]() =
=![]() ;
;
当a=2时,![]() =
=![]() ;
;
∴点![]() 的坐标是
的坐标是![]() 或
或![]() .
.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目