题目内容
【题目】如图,已知A是双曲线y= ![]() (k>0)在第一象限内的一点,O为坐标原点,直线OA交双曲线于另一点C,当OA在第一象限的角平分线上时,将OA向上平移
(k>0)在第一象限内的一点,O为坐标原点,直线OA交双曲线于另一点C,当OA在第一象限的角平分线上时,将OA向上平移 ![]() 个单位后,与双曲线在第一象限交于点M,交y轴于点N,若
个单位后,与双曲线在第一象限交于点M,交y轴于点N,若 ![]() =2,
=2,
(1)求直线MN的解析式;
(2)求k的值.
【答案】
(1)解:∵OA在第一象限的角平分线上,
∴直线OA的解析式为y=x,
∴将OA向上平移 ![]() 个单位后,N(0,
个单位后,N(0, ![]() ),
),
可设直线MN的解析式为y=x+b,
把N(0, ![]() )代入,可得b=
)代入,可得b= ![]() ,
,
∴直线MN的解析式为y=x+ ![]()
(2)解:如图所示,过A作AB⊥y轴于B,过M作MD⊥y轴于D,则∠MDN=∠ABO=90°,
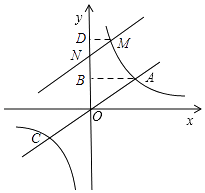
由平移可得,∠MND=∠AOB=45°,
∴△MDN∽△ABO,
∴ ![]() =
= ![]() =2,
=2,
设A(a,a),则AB=a,
∴MD= ![]() a=DN,
a=DN,
∴DO= ![]() a+
a+ ![]() ,
,
∴M( ![]() a,
a, ![]() a+
a+ ![]() ),
),
∵双曲线经过点A,M,
∴k=a×a= ![]() a×(
a×( ![]() a+
a+ ![]() ),
),
解得a=1,
∴k=1.
【解析】(1)第一三象限角平分线为y=x,向上平移为y=x+b,可求出N点坐标,代入y=x+b,即可求出;(2)通过作垂线构造相似三角形,即△MDN∽△ABO,把A、M坐标代入解析式即可求出a,进而求出k.

练习册系列答案
相关题目
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.