题目内容
【题目】定义:如果一个三角形的一个内角等于另一个内角的两倍,则称这样的三角形为“倍角三角形”.
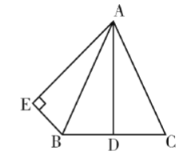
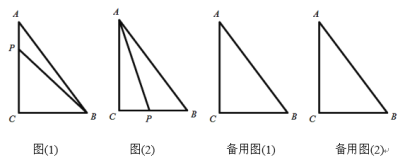
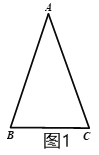
(1)如图1,△ABC中,AB=AC,∠A为36°,求证:△ABC 是锐角三角形;
(2)若△ABC是倍角三角形,![]() ,∠B=30°,AC=
,∠B=30°,AC=![]() ,求△ABC面积;
,求△ABC面积;
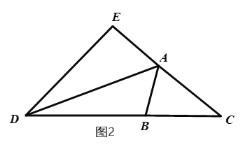
(3)如图2,△ABC的外角平分线AD与CB的延长线相交于点D,延长CA到点E,使得AE=AB,若AB+AC=BD,请你找出图中的倍角三角形,并进行证明.
【答案】(1)证明见解析;(2)![]() ;(3)△ADC是倍角三角形,证明见解析.
;(3)△ADC是倍角三角形,证明见解析.
【解析】
(1)根据题意证明△ABC是等腰三角形,得出三个内角的度数,得证△ABC 是锐角三角形
(2)分两种情况讨论,①当∠B=2∠C②当∠A=2∠B或∠A=2∠C时,求出△ABC面积
(3)证明△ABD≌△AED,从而证明CE=DE,∠C=∠BDE=2∠ADC,△ADC是倍角三角形
(1)∵AB=AC,∴∠B=∠C
∵∠A+∠B+∠C=180°,∠A=36°
∴∠B=∠C=72°
∴∠A=2∠C
即△ABC是锐角三角形
(2)∵∠A>∠B>∠C,∠B=30°
①当∠B=2∠C,得∠C=15°
过C作CH⊥直线AB,垂足为H,

可得∠CAH=45°
∴AH=CH=![]() AC=4.
AC=4.
∴BH=![]()
∴AB=BH-AH=![]() -4
-4
∴S=![]()
②当∠A=2∠B或∠A=2∠C时,与∠A>∠B>∠C矛盾,故不存在。
综上所述,△ABC面积为![]()
(3)∵AD平分∠BAE,
∴∠BAD=∠EAD
∵AB=AE,AD=AD,
∴△ABD≌△AED.
∴∠ADE=∠ADB,BD=DE.
又∵AB+AC=BD,
∴AE+AC=BD,即CE=BD.
∴CE=DE.
∴∠C=∠BDE=2∠ADC.
∴△ADC是倍角三角形.

练习册系列答案
相关题目