题目内容
【题目】阅读下面方法,解答后面的问题:
(阅读理解)我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用。
例题:已知x可取任意实数,试求二次三项式![]() 的取值范围。
的取值范围。
解: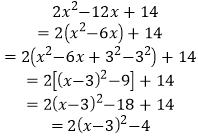
∵x取任何实数,总有![]() ,∴
,∴![]() 。
。
因此,无论x取任何实数,![]() 的值总是不小于-4的实数。
的值总是不小于-4的实数。
特别的,当x=3时,![]() 有最小值-4
有最小值-4
(应用1):已知x可取任何实数,则二次三项式![]() 的最值情况是( )
的最值情况是( )
A. 有最大值-10 B. 有最小值-10 C. 有最大值-7 D. 有最小值-7
(应用2):某品牌服装进货价为每件50元,商家在销售中发现:当以每件90元销售时,平均每天可售出20件,为了扩大销售量,增加盈利,商家决定采取适当的降价措施。
(1)将市场调查发现:如果每件服装降价1元,那么平均每天那就可多售出2件,要想平均每天销售这种服装盈利为1200元,我们设降价x元,根据题意列方程得( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
(2)请利用上面(阅读理解)提供的方法解决下面问题:
这家服装专柜为了获得每天的最大盈利,每件服装需要降价多少元?每天的最大盈利又是多少元?
【答案】【应用1】B ;【应用2】(1)A;(2)降价15元时,每天的盈利最大,每天的最大盈利是1250元.
【解析】
应用1、根据配方法求出其顶点式,即可得出即可;
应用2、(1)根据题意中的等量关系列出方程即可;
(2)根据(1)中的方程,将其转化为顶点式即可得出结论.
应用1、B
应用2、(1)A
(2)![]()
∵![]() ∴
∴![]()
特别的,当x=15时,![]() 有最大值1250
有最大值1250
∴降价15元时,每天的盈利最大,每天的最大盈利是1250元。

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目