题目内容
如图1,矩形纸片ABCD中,AD=14cm,AB=10cm.(1)将矩形纸片ABCD沿折线AE对折,使AB边与AD边重合,B点落在F点处,如图2所示;再剪去四边形CEFD,余下的部分如图所示.若将余下的纸片展开,则所得的四边形ABEF的形状是
(2)将图3中的纸片沿折线AG对折,使AF与AE边重合,F点落在H点处,如图4所示;再沿HG将△HGE剪去,余下的部分如图5所示.
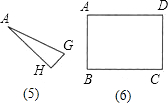
把图5的纸片完全展开,请你在图6的矩形ABCD中画出展开后图形的示意图,剪去的部分用阴影表示,折痕用虚线表示;
(3)求图5中的纸片完全展开后的图形面积(结果保留整数).
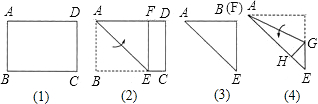
分析:(1)根据翻折变换的性质,结合正方形的定义,推出四边形ABEF为正方形,面积即AB2;
(2)根据题意中翻折变换的步骤进行画图即可;
(3)根据题意推出AB=AH=AF=10,GH=HE,根据三角形的面积公式求出图5中的纸片完全展开后的图形面积.
(2)根据题意中翻折变换的步骤进行画图即可;
(3)根据题意推出AB=AH=AF=10,GH=HE,根据三角形的面积公式求出图5中的纸片完全展开后的图形面积.
解答:解:(1)正方形;100;
(2)如图

(3)AE=1O
,HE=10
-10,
GH=HE,S≈8.6(cm2)
∴S多边形≈83(cm2)
答:图5中的纸片完全展开后的图形面积为83cm2.
(2)如图

(3)AE=1O
| 2 |
| 2 |
GH=HE,S≈8.6(cm2)
∴S多边形≈83(cm2)
答:图5中的纸片完全展开后的图形面积为83cm2.
点评:本题主要考查了矩形的性质、翻折变换的性质、等腰三角形的性质等知识点,关键在于根据题意翻折变换出图形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 13、如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
13、如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E. (2013•松北区三模)如图,将矩形纸片ABCD折痕,使点D落在点线段AB的中点F处.若AB=4,则边BC的长为( )
(2013•松北区三模)如图,将矩形纸片ABCD折痕,使点D落在点线段AB的中点F处.若AB=4,则边BC的长为( ) 如图,把矩形纸片ABCD沿折叠,使点B落在边AD上的点B′处,点A落在点A′处;
如图,把矩形纸片ABCD沿折叠,使点B落在边AD上的点B′处,点A落在点A′处; 17、如图,将矩形纸片ABCD沿EF折叠,点C与点A重合,点D落在点D′处,已知AB=4,BC=8,则线段AE的长度是
17、如图,将矩形纸片ABCD沿EF折叠,点C与点A重合,点D落在点D′处,已知AB=4,BC=8,则线段AE的长度是
