题目内容
 如图,把矩形纸片ABCD沿折叠,使点B落在边AD上的点B′处,点A落在点A′处;
如图,把矩形纸片ABCD沿折叠,使点B落在边AD上的点B′处,点A落在点A′处;( I)求证:B′E=BF
( II)设AE=a,AB=b,BF=c,求证:a+b>c.
分析:(I)连接BE,利用△BEF和△B'EF是轴对称图形得出∠B'FE=∠BFE,BF=B′F,进而得出∠B′EF=∠B′FE,即可得出答案;
(II)利用(I)中结论,即可得出AE=A′E=a,AB=A′B′=b,BF=B′E=c,再利用三角形三边关系得出即可.
(II)利用(I)中结论,即可得出AE=A′E=a,AB=A′B′=b,BF=B′E=c,再利用三角形三边关系得出即可.
解答:(I)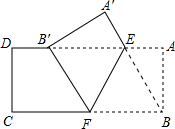 证明:连接BE,
证明:连接BE,
∵△BEF和△B'EF是轴对称图形.
则∠B'FE=∠BFE,BF=B′F,
∵AD∥BC,
∴∠B′EF=∠EFB,
∴∠B′EF=∠B′FE,
∴B′F=B′E,
∴B′E=BF;
(II)证明:∵B′E=BF,A′E=AE,AB=A′B′,
∴AE=A′E=a,AB=A′B′=b,BF=B′E=c,
∵在△A′B′E中,
A′B′+A′E>B′E,
∴a+b>c.
 证明:连接BE,
证明:连接BE,∵△BEF和△B'EF是轴对称图形.
则∠B'FE=∠BFE,BF=B′F,
∵AD∥BC,
∴∠B′EF=∠EFB,
∴∠B′EF=∠B′FE,
∴B′F=B′E,
∴B′E=BF;
(II)证明:∵B′E=BF,A′E=AE,AB=A′B′,
∴AE=A′E=a,AB=A′B′=b,BF=B′E=c,
∵在△A′B′E中,
A′B′+A′E>B′E,
∴a+b>c.
点评:此题主要考查了翻折变换的性质以及三角形三边关系,利用已知得出∠B′EF=∠B′FE进而求出B′F=B′E是解题关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 22、如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;
22、如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处; (2009•自贡)如图,把矩形纸片ABCD沿EF折叠,使点B落在AD边上的点B′处,点A落在A′处.
(2009•自贡)如图,把矩形纸片ABCD沿EF折叠,使点B落在AD边上的点B′处,点A落在A′处. 如图,把矩形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把矩形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上. 如图,把矩形纸片ABCD沿着EF折叠,使点B落在边AD上的点D处.点A落在点A′.
如图,把矩形纸片ABCD沿着EF折叠,使点B落在边AD上的点D处.点A落在点A′. 10、如图,把矩形纸片ABCD沿EF折叠,使点B落在AD边上的点B′处,点A落在点A′处.设AE=a,AB=b,BF=c,下列结论:
10、如图,把矩形纸片ABCD沿EF折叠,使点B落在AD边上的点B′处,点A落在点A′处.设AE=a,AB=b,BF=c,下列结论: