题目内容
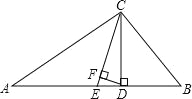
【题目】如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90°后,得到△AFC,连接DF.
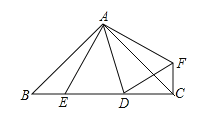
(1)试说明:△AED≌△AFD;
(2)当BE=3,CE=9时,求∠BCF的度数和DE的长;
【答案】(1)见解析;(2)90°,5.
【解析】
(1)根据旋转的性质,可得对应角与对应边相等;根据全等三角形的判定定理即可证明;
(2)设DE=x,则CD=9﹣x.在Rt△DCF中,由DF2=CD2+CF2,CF=BE=3,推出x2=(9﹣x)2+32,解方程即可.
(1)证明:∵将△ABE绕点A逆时针旋转90°后,得到△AFC,
∴△BAE≌△CAF,
∴AE=AF,∠BAE=∠CAF,BE=CF,
∵∠BAC=90°,∠EAD=45°,
∴∠CAD+∠BAE=∠CAD+∠CAF=45°,
∴∠DAE=∠DAF,
∵DA=DA,AE=AF,
∴△AED≌△AFD(SAS);
(2)解:设DE=x,则CD=9﹣x.
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵∠ABE=∠ACF=45°,
∴∠BCF=90°,
∵△AED≌△AFD,
∴DE=DF=x,
在Rt△DCF中,∵DF2=CD2+CF2,CF=BE=3,
∴x2=(9﹣x)2+32,
∴x=5,
∴DE=5.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目