题目内容
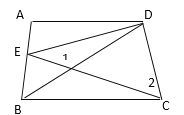
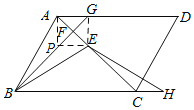
【题目】如图,在ABCD中,∠ACB=45°,点E在对角线AC上,BE=BA,BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG,连接EH.
(1)若BC=12![]() ,AB=13,求AF的长;
,AB=13,求AF的长;
(2)求证:EB=EH.

【答案】(1)5;(2)证明见解析.
【解析】
(1)依据BF⊥AC,∠ACB=45°,BC=12![]() ,可得等腰Rt△BCF中,BF=sin45°×BC=12,再根据勾股定理,即可得到Rt△ABF中,AF=
,可得等腰Rt△BCF中,BF=sin45°×BC=12,再根据勾股定理,即可得到Rt△ABF中,AF=![]() =5;
=5;
(2)连接GE,过A作AF⊥AG,交BG于P,连接PE,判定四边形APEG是正方形,即可得到PF=EF,AP=AG=CH,进而得出△APB≌△HCE,依据AB=EH,AB=BE,即可得到BE=EH.
解:(1)如图,∵BF⊥AC,∠ACB=45°,BC=12![]() ,
,
∴等腰Rt△BCF中,BF=sin45°×BC=12,
又∵AB=13,
∴Rt△ABF中,AF=![]() =5;
=5;
(2)如图,连接GE,过A作AF⊥AG,交BG于P,连接PE,
∵BE=BA,BF⊥AC,
∴AF=FE,
∴BG是AE的垂直平分线,
∴AG=EG,AP=EP,
∵∠GAE=∠ACB=45°,
∴△AGE是等腰直角三角形,即∠AGE=90°,
△APE是等腰直角三角形,即∠APE=90°,
∴∠APE=∠PAG=∠AGE=90°,
又∵AG=EG,
∴四边形APEG是正方形,
∴PF=EF,AP=AG=CH,
又∵BF=CF,
∴BP=CE,
∵∠APG=45°=∠BCF,
∴∠APB=∠HCE=135°,
∴△APB≌△HCE(SAS),
∴AB=EH,
又∵AB=BE,
∴BE=EH.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目