题目内容
【题目】如图,在△ABC中,AB=AC,D在边BC上,以A为圆心,AD长为半径画圆弧,交边BC的另一点E,交边AC于F,连接AE,EF. 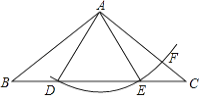
(1)求证:△ABD≌△ACE;
(2)若∠ADB=3∠CEF,请判断EF与AB有怎样的位置关系?并说明理由.
【答案】
(1)证明:由题意可知AD=AE=AF,
∴∠ADE=∠AED,
∴∠ADB=∠AEC,
∵AB=AC,
∴∠B=∠C,
在△ABD和△ACD中, 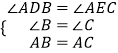 ,
,
∴△ABD≌△ACD;
(2)解:∵∠ADB=∠AEC,∠ADB=3∠CEF,
∴∠AEF=2∠CEF,
∵AE=AF,
∴∠AFE=∠AEF=2∠CEF,
∴∠CEF=∠C,
∵△ABD≌△ACD,
∴∠B=∠C,
∴∠CEF=∠B,
∴EF∥AB.
【解析】(1)根据全等三角形的判定定理得到△ABD≌△ACD;(2)根据已知条件得到∠AEF=2CEF,根据等腰三角形的性质得到∠AFE=∠AEF=2∠CEF,等量代换得到∠CEF=∠C,根据全等三角形的性质得到∠B=∠C,于是得到结论;
【考点精析】通过灵活运用直线与圆的三种位置关系,掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点即可以解答此题.

 名校课堂系列答案
名校课堂系列答案【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利情况如表所示:
销售方式 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 1000 | 2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工. ①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?