题目内容
已知:二次函数y=ax2+bx+c(a>0)的图象与x轴交于A(1,0)、B(5,0),抛物线的顶点为P,且PB=2| 5 |
(1)二次函数的解析式;
(2)画出这个二次函数的图象;
(3)根据图象回答:当x取什么值时,y的值不小于0.
分析:(1)设二次函数的解析式为y=a(x-1)(x-5),即y=ax2-6ax+5a,根据二次函数的对称轴公式可知对称轴为x=3,所以OC=3,BC=2,由BP=2
可知PC=4,即P(3,-4),利用待定系数法可求得a=
,所以二次函数的解析式为y=
x2-
+
;
(2)利用列表,描点,连线的方法画图即可;
(3)在图象上当图象在x轴上方时y的值不小于0,所以x≤1或x≥5时,y≥0.
| 5 |
| 19 |
| 9 |
| 19 |
| 9 |
| 144 |
| 9 |
| 95 |
| 9 |
(2)利用列表,描点,连线的方法画图即可;
(3)在图象上当图象在x轴上方时y的值不小于0,所以x≤1或x≥5时,y≥0.
解答:解:(1)由题意,设二次函数的解析式为y=a(x-1)(x-5),
即y=ax2-6ax+5a.
对称轴为x=3,设对称轴与x轴的交点为C(3,0).
∴OC=3.
∵OB=5,
∴BC=2.
∵P是顶点,BP=2
,
∴PC=4,P(3,-4).
∴a×32-6a×3+5×3=-4,
∴a=1.
∴二次函数的解析式为y=x2-6x+5.
(2)如图:

(3)当x≤1或x≥5时,y≥0.
即y=ax2-6ax+5a.
对称轴为x=3,设对称轴与x轴的交点为C(3,0).
∴OC=3.
∵OB=5,
∴BC=2.
∵P是顶点,BP=2
| 5 |
∴PC=4,P(3,-4).
∴a×32-6a×3+5×3=-4,
∴a=1.
∴二次函数的解析式为y=x2-6x+5.
(2)如图:

(3)当x≤1或x≥5时,y≥0.
点评:本题考查二次函数的综合应用,其中涉及到的知识点有待定系数法求函数解析式,画二次函数图象以及图象性质的运用等.要熟练掌握才能灵活运用.

练习册系列答案
相关题目
 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.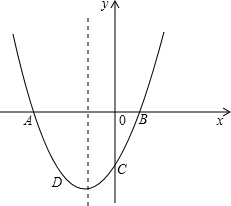 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.