题目内容
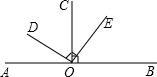
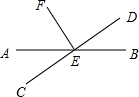
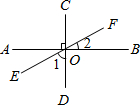
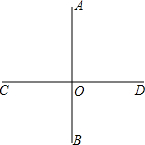
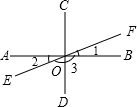
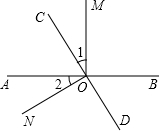
如图，直线AB、CD相交于点O，OM⊥AB．
（1）若∠1=∠2，求∠NOD．
（2）若∠1=
∠BOC，求∠AOC与∠MOD．
（1）若∠1=∠2，求∠NOD．
（2）若∠1=
| 1 |
| 3 |
（1）∵OM⊥AB，
∴∠AOM=∠1+∠AOC=90°，
∵∠1=∠2，
∴∠NOC=∠2+∠AOC=90°，
∴∠NOD=180°-∠NOC=180°-90°=90°；
（2）∵OM⊥AB，
∴∠AOM=∠BOM=90°，
∵∠1=
∠BOC，
∴∠BOC=∠1+90°=3∠1，
解得∠1=45°，
∠AOC=90°-∠1=90°-45°=45°，
∠MOD=180°-∠1=180°-45°=135°．
∴∠AOM=∠1+∠AOC=90°，
∵∠1=∠2，
∴∠NOC=∠2+∠AOC=90°，
∴∠NOD=180°-∠NOC=180°-90°=90°；
（2）∵OM⊥AB，
∴∠AOM=∠BOM=90°，
∵∠1=
| 1 |
| 3 |
∴∠BOC=∠1+90°=3∠1，
解得∠1=45°，
∠AOC=90°-∠1=90°-45°=45°，
∠MOD=180°-∠1=180°-45°=135°．
练习册系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
