题目内容
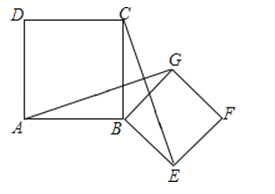
【题目】已知:如图,四边形ABCD是平行四边形,DE∥AC,交BC的延长线于点E,EF⊥AB于点F,求证:AD=CF.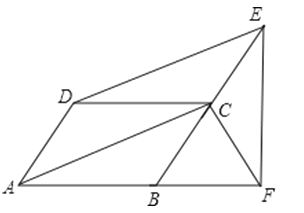
【答案】证明:∵DE∥AC,
∴∠DEC=∠ACB,∠EDC=∠DCA,
∵四边形ABCD是平行四边形,
∴∠CAB=∠DCA,
∴∠EDC=∠CAB,
又∵AB=CD,
∴△EDC≌△CAB,
∴CE=CB,
所以在Rt△BEF中,FC为其中线,
所以FC=BC,
即FC=AD.
【解析】利用平行四边形及平行线证明△EDC≌△CAB,可得BC=CE,即FC为直角三角形的中线,由直角三角形的性质即可得出结论.
【考点精析】掌握平行四边形的性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目