题目内容
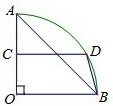 如图,在扇形OAB中,∠AOB=90°,C为OA的中点,点D在
如图,在扇形OAB中,∠AOB=90°,C为OA的中点,点D在 | AB |
分析:根据在直角三角形中所对的边等于斜边的一半,得出∠CDO=30°,进而得出∠COD=60°,再利用圆周角定理求出即可.
解答: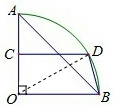 解:连接DO,
解:连接DO,
∵∠AOB=90°,C为OA的中点,
∴2CO=DO,
∴∠CDO=30°,
∴∠COD=60°,
根据圆周角定理可得:∠ABD=30°.
故答案为:30°.
 解:连接DO,
解:连接DO,∵∠AOB=90°,C为OA的中点,
∴2CO=DO,
∴∠CDO=30°,
∴∠COD=60°,
根据圆周角定理可得:∠ABD=30°.
故答案为:30°.
点评:此题主要考查了圆周角定理以及含30°角直角三角形,根据题意得出2CO=DO,进而得出∠CDO=30°是解决问题的关键.

练习册系列答案
相关题目
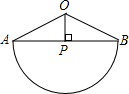 如图,在扇形OAB中,OP⊥AB于点P,半径为4,OP=2.
如图,在扇形OAB中,OP⊥AB于点P,半径为4,OP=2.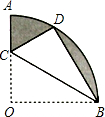 (2012•吉林)如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在
(2012•吉林)如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在 如图,在扇形OAB中,∠AOB=110°,半径OA=12,将扇形OAB沿过点B的直线折叠,点O恰好落在
如图,在扇形OAB中,∠AOB=110°,半径OA=12,将扇形OAB沿过点B的直线折叠,点O恰好落在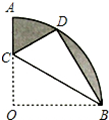 (2013•平顶山二模)如图,在扇形OAB中,∠AOB=90°,半径OA=6.将沿过点B的直线折叠,点O恰好落
(2013•平顶山二模)如图,在扇形OAB中,∠AOB=90°,半径OA=6.将沿过点B的直线折叠,点O恰好落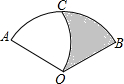 (2013•老河口市模拟)如图,在扇形OAB中,∠AOB=120°,OA=2,以A为圆心,AO长为半径画弧交
(2013•老河口市模拟)如图,在扇形OAB中,∠AOB=120°,OA=2,以A为圆心,AO长为半径画弧交