题目内容
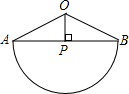 如图,在扇形OAB中,OP⊥AB于点P,半径为4,OP=2.
如图,在扇形OAB中,OP⊥AB于点P,半径为4,OP=2.(1)求AB的长;
(2)求∠AOB的度数;
(3)求扇形OAB的面积.
分析:(1)根据垂径定理可知AB=2AP,在Rt△OAP中利用勾股定理即可求得AP的长度,从而求得AB的长;
(2)利用Rt△OAP中的三角函数可求得∠AOP=60°,根据垂径定理可知∠AOB=2∠AOP=120°;
(3)利用前2问,代入扇形的面积公式求解即可.
(2)利用Rt△OAP中的三角函数可求得∠AOP=60°,根据垂径定理可知∠AOB=2∠AOP=120°;
(3)利用前2问,代入扇形的面积公式求解即可.
解答:解:(1)∵OP⊥AB于点P,
∴AB=2AP
在Rt△OAP中,
AP=
=
=2
∴AB=2AP=4
;
(2)∵在Rt△OAP中,cos∠AOP=
=
=
∴∠AOP=60°
∴∠AOB=2∠AOP=120°;
(3)∴S扇形OAB=
=
∴扇形OAB的面积是
.
∴AB=2AP
在Rt△OAP中,

AP=
| OA2-OP2 |
| 42-22 |
| 3 |
∴AB=2AP=4
| 3 |
(2)∵在Rt△OAP中,cos∠AOP=
| OP |
| OA |
| 2 |
| 4 |
| 1 |
| 2 |
∴∠AOP=60°
∴∠AOB=2∠AOP=120°;
(3)∴S扇形OAB=
| 120•π•42 |
| 360 |
| 16π |
| 3 |
∴扇形OAB的面积是
| 16π |
| 3 |
点评:主要考查了垂径定理的运用和扇形的面积公式.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧(进而可推出还平分弦所对的圆心角).牢记扇形的面积公式:S=
.
| nπ r2 |
| 360 |

练习册系列答案
相关题目
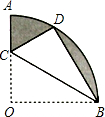 (2012•吉林)如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在
(2012•吉林)如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在
 如图,在扇形OAB中,∠AOB=110°,半径OA=12,将扇形OAB沿过点B的直线折叠,点O恰好落在
如图,在扇形OAB中,∠AOB=110°,半径OA=12,将扇形OAB沿过点B的直线折叠,点O恰好落在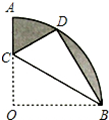 (2013•平顶山二模)如图,在扇形OAB中,∠AOB=90°,半径OA=6.将沿过点B的直线折叠,点O恰好落
(2013•平顶山二模)如图,在扇形OAB中,∠AOB=90°,半径OA=6.将沿过点B的直线折叠,点O恰好落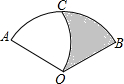 (2013•老河口市模拟)如图,在扇形OAB中,∠AOB=120°,OA=2,以A为圆心,AO长为半径画弧交
(2013•老河口市模拟)如图,在扇形OAB中,∠AOB=120°,OA=2,以A为圆心,AO长为半径画弧交