题目内容
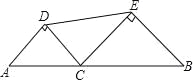
【题目】如图,AB是⊙O的直径,点C在⊙O上,连接AC,BC,OE⊥AC于点E,ED∥AB交BC于点F,且∠BCD=∠A
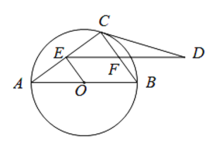
(1)求证:CD是⊙O的切线;
(2)求证:![]() ;
;
(3)若![]() ,BC=6,求CD的长
,BC=6,求CD的长
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连接OC,证明∠OCA+∠BCO=90°,∠OCA=∠BCD,得到OC⊥CD,问题得证;
(2)证明∠CED=∠FCD,证明△CFD∽△ECD,根据相似性质即可证明;
(3)求出AB、AC、CE、CF,根据(2),证明CD∶ED=FD∶CD=3∶4,设![]() ,则
,则![]() 根据
根据![]() 列方程,解方程即可.
列方程,解方程即可.
解:(1)连接OC.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠OCA+∠BCO=90°,
∵OA=OC,
∴∠OCA=∠A,
∵∠BCD=∠A,
∴∠OCA=∠BCD,
∴∠BCD+∠BCO=90°,
即∠DCO=90°,
∴OC⊥CD,
∴CD是⊙O的切线;
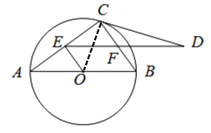
(2)∵ED∥AB,
∴∠CED=∠A,
∵∠FCD=∠A,
∴∠CED=∠FCD,
∵∠D=∠D,
∴△CFD∽△ECD,
∴![]() ,
,
即![]() ,
,
(3)Rt△ACB中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵OE⊥AC,
∴![]() ,
,
∵EF∥AB,
∴△CEF∽△CAB,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
由(2)知△CFD∽△ECD ,
∴![]() ,
,
即![]() ,
,
设![]() ,则
,则![]() ,
,
由![]() 得,
得,
![]() ,
,
解得:![]() ,
,
∴![]() .
.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20