Question

【题目】如图，经过原点的抛物线y=﹣x2﹣2mx（m＞1）与x轴的另一个交点为A．过点P（﹣1，m）作直线PD⊥x轴于点D，交抛物线于点B，BC∥x轴交抛物线于点C．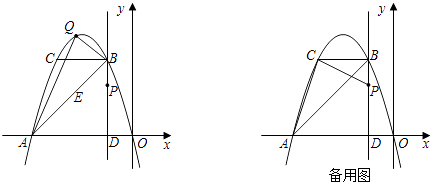

（1）当m=2时．
①求线段BC的长及直线AB所对应的函数关系式；
②若动点Q在直线AB上方的抛物线上运动，求点Q在何处时，△QAB的面积最大？
③若点F在坐标轴上，且PF=PC，请直接写出符合条件的点F在坐标；
（2）当m＞1时，连接CA、CP，问m为何值时，CA⊥CP？

Answer 1

【答案】
（1）

解：①当m=2时，y=﹣x2﹣4x，

令y=0，得﹣x2﹣4x=0，

解得x1=0，x2=﹣4，

则A（﹣4，0）．

当x=﹣1时，y=3，

则B（﹣1，3）．

∵抛物线y=﹣x2﹣4x的对称轴为直线x=﹣2，

∴B、C两点关于对称轴x=﹣2对称，

∴C（﹣3，3），BC=2．

设直线AB所对应的函数关系式为y=kx+b．

∵A（﹣4，0）、B（﹣1，3）在直线AB上，

∴ ，

解得

∴直线AB所对应的函数关系式为y=x+4；

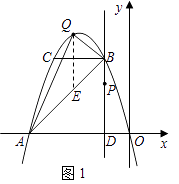
②过点Q作QE∥y轴，交AB于点E（如图1）．

由题意可设Q（a，﹣a2﹣4a），则E（a，a+4），

∴QE=（﹣a2﹣4a）﹣（a+4）=﹣a2﹣5a﹣4．

∴S△QAB= QEAD

= ×（﹣a2﹣5a﹣4）×3

=﹣ （a+ ）2+ ，

∴当a= 时，△QAB的面积最大，此时Q的坐标为（ ， ）；

③分两种情况：

若点F在x轴上，设F（x，0）．

∵PF=PC，P（﹣1，2），C（﹣3，3），

∴（x+1）2+（2﹣0）2=（﹣3+1）2+（3﹣2）2，

整理，得x2+2x=0，

解得x1=﹣2，x2=0，

∴F1（﹣2，0），F2（0，0）；

若点F在y轴上，设F（0，y）．

∵PF=PC，P（﹣1，2），C（﹣3，3），

∴（0+1）2+（y﹣2）2=（﹣3+1）2+（3﹣2）2，

整理，得y2﹣4y=0，

解得y1=4，y2=0，

∴F3（0，4），F4（0，0）与F2（0，0）重合；

综上所述，符合条件的点F坐标为F1（﹣2，0），F2（0，0），F3（0，4）

（2）

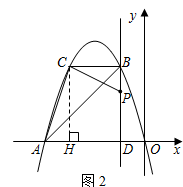
解：过点C作CH⊥x轴于点H（如图2）．

∵P（﹣1，m），B（﹣1，2m﹣1），

∴PB=m﹣1．

∵抛物线y=﹣x2﹣2mx的对称轴为直线x=﹣m，其中m＞1，

∴B、C两点关于对称轴x=﹣m对称，

∴BC=2（m﹣1），

∴C（1﹣2m，2m﹣1），H（1﹣2m，0），

∴CH=2m﹣1，

∵A（﹣2m，0），

∴AH=1．

由已知，得∠ACP=∠BCH=90°，

∴∠ACH=∠PCB．

又∵∠AHC=∠PBC=90°，

∴△ACH∽△PCB，

∴ ，即 ，

∴m=

【解析】（1）①将m=2代入y=﹣x2﹣2mx，得出y=﹣x2﹣4x，求出A（﹣4，0），B（﹣1，3），由B、C两点关于抛物线y=﹣x2﹣4x的对称轴x=﹣2对称，得出BC=2，运用待定系数法求出直线AB所对应的函数关系式；②过点Q作QE∥y轴，交AB于点E，设Q（a，﹣a2﹣4a），则E（a，a+4），QE=（﹣a2﹣4a）﹣（a+4）=﹣a2﹣5a﹣4，由S△QAB= QEAD求出S△QAB=﹣ （a+ ）2+ ，根据二次函数的性质即可求解；③分两种情况进行讨论：若点F在x轴上，设F（x，0）．根据PF=PC列出方程，解方程得到F1（﹣2，0），F2（0，0）；若点F在y轴上，设F（0，y），根据PF=PC列出方程，解方程得到F3（0，4），F4（0，0）与F2（0，0）重合；（2）过点C作CH⊥x轴于点H．先求出PB=m﹣1，BC=2（m﹣1），CH=2m﹣1，AH=1，再证明△ACH∽△PCB，根据相似三角形对应边成比例得出 ，即 ，解方程可求出m的值．
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本，需要知道二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．