Question

【题目】要测量旗杆高CD ， 在B处立标杆AB=2.5cm，人在F处．眼睛E、标杆顶A、旗杆顶C在一条直线上．已知BD=3.6m，FB=2.2m，EF=1.5m．求旗杆的高度．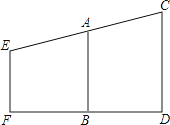

Answer 1

【答案】解答：过E作EH∥FD分别交AB、CD于G、H ．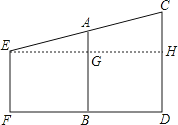

因为EF∥AB∥CD ， 所以EF=GB=HD ．
所以AG=AB-GB=AB-EF=2.5-1.5=1m
EG=FB=2.2m，GH=BD=3.6m
CH=CD-1.5m
又因为 ＝ ，
所以 ＝
所以CD=4 m，即旗杆的高4 m
【解析】过E作EH∥FD分别交AB、CD于G、H ， 根据EF∥AB∥CD可求出AG、EG、GH ， 再根据相似三角形的判定定理可得△EAG∽△ECH ， 再根据三角形的相似比解答即可．
【考点精析】本题主要考查了相似三角形的应用的相关知识点，需要掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解才能正确解答此题．