题目内容
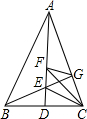 如图,△ABC中AB=AC,AD⊥BC,垂足为点D,∠BAC=48°,CE、CF三等分∠ACB,分别交AD于点E、F,连接BE并延长交AC于点G,连接FG,则∠AGF=
如图,△ABC中AB=AC,AD⊥BC,垂足为点D,∠BAC=48°,CE、CF三等分∠ACB,分别交AD于点E、F,连接BE并延长交AC于点G,连接FG,则∠AGF=分析:设BG与CF交点为O,连接BF,根据等腰三角形的性质得到BD=DC,推出∠FBE=∠FCE,由FBE=∠FCE=∠FCG,证出△FOB∽△GOC,得出
=
,进一步推出△FOG∽△BOC,得到∠FGO=∠BCO=44°,根据∠AGF=∠BGA-∠FGO即可求出答案.
| FO |
| BO |
| GO |
| CO |
解答: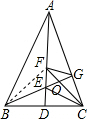 解:∵∠A=48°,AC=AB,
解:∵∠A=48°,AC=AB,
∴∠ABC=∠ACB=
(180°-∠BAC)=66°,
设BG与CF交点为O,连接BF,
∵AB=AC,AD⊥BC,
∴BD=DC,
∴FB=FC,
∴∠FBC=∠FCB,
同理∠EBC=∠ECB,
∴∠FBE=∠FCE,
∵CE,CF三等分∠GCD,
∴∠FBE=∠FCE=∠FCG,
∵∠FOB=∠GOC,
∴△FOB∽△GOC,
∴
=
,
∵∠FOG=∠BOC
∴△FOG∽△BOC
∴∠FGO=∠BCO=
∠ACB=
×66°=44°
∴∠AGF=∠BGA-∠FGO,
=∠GBC+∠GCB-∠FGO,
=22°+66°-44°=44°.
故答案为:44°.
 解:∵∠A=48°,AC=AB,
解:∵∠A=48°,AC=AB,∴∠ABC=∠ACB=
| 1 |
| 2 |
设BG与CF交点为O,连接BF,
∵AB=AC,AD⊥BC,
∴BD=DC,
∴FB=FC,
∴∠FBC=∠FCB,
同理∠EBC=∠ECB,
∴∠FBE=∠FCE,
∵CE,CF三等分∠GCD,
∴∠FBE=∠FCE=∠FCG,
∵∠FOB=∠GOC,
∴△FOB∽△GOC,
∴
| FO |
| BO |
| GO |
| CO |
∵∠FOG=∠BOC
∴△FOG∽△BOC
∴∠FGO=∠BCO=
| 2 |
| 3 |
| 2 |
| 3 |
∴∠AGF=∠BGA-∠FGO,
=∠GBC+∠GCB-∠FGO,
=22°+66°-44°=44°.
故答案为:44°.
点评:本题主要考查对等腰三角形的性质,相似三角形的性质和判定,线段的垂直平分线,角平分线的定义等知识点的理解和掌握,能正确利用这些性质进行推理是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
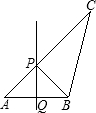 如图,△ABC中AB的垂直平分线交AC、AB于点P、Q,若PC=2PA,AB=
如图,△ABC中AB的垂直平分线交AC、AB于点P、Q,若PC=2PA,AB=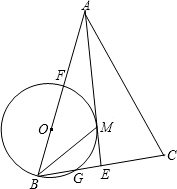 交BC于G,交AB于点F,FB恰为⊙O的直径.
交BC于G,交AB于点F,FB恰为⊙O的直径.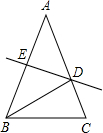 如图,△ABC中AB=AC,AB的垂直平分线交AC于点D.若∠A=40°,则∠DBC=
如图,△ABC中AB=AC,AB的垂直平分线交AC于点D.若∠A=40°,则∠DBC= 15、如图,△ABC中AB=AC,∠A=36°,AB的垂直平分线MN交AC于D,下列四个结论正确的是
15、如图,△ABC中AB=AC,∠A=36°,AB的垂直平分线MN交AC于D,下列四个结论正确的是 15、如图,△ABC中AB=AC,EB=BD=DC=CF,∠A=40°,则∠EDF的度数是
15、如图,△ABC中AB=AC,EB=BD=DC=CF,∠A=40°,则∠EDF的度数是