题目内容
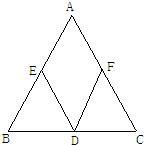15、如图，△ABC中AB=AC，EB=BD=DC=CF，∠A=40°，则∠EDF的度数是70
度．分析：利用等腰三角形的性质及三角形内角和定理先求出∠B、∠C的度数，再根据等腰三角形求出底角∠BDE和∠CDF的度数，根据平角定义即可求解．
解答：解：∵AB=AC，∠A=40°
∴∠B=∠C=70°
∵EB=BD=DC=CF
∴∠BDE=（180°-70°）÷2=55°，∠CDF=（180°-70°）÷2=55°
∴∠EDF=180°-55°-55°=70°．
故填70．
∴∠B=∠C=70°
∵EB=BD=DC=CF
∴∠BDE=（180°-70°）÷2=55°，∠CDF=（180°-70°）÷2=55°
∴∠EDF=180°-55°-55°=70°．
故填70．
点评：本题考查了等腰三角形的性质及三角形内角和定理；注意发现三个等腰三角形，根据等腰三角形的两个底角相等以及三角形的内角和定理进行求解是解答本题的关键．
练习册系列答案
相关题目
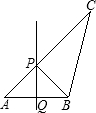如图，△ABC中AB的垂直平分线交AC、AB于点P、Q，若PC=2PA，AB=
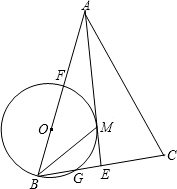交BC于G，交AB于点F，FB恰为⊙O的直径．
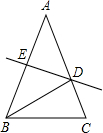如图，△ABC中AB=AC，AB的垂直平分线交AC于点D．若∠A=40°，则∠DBC=
15、如图，△ABC中AB=AC，∠A=36°，AB的垂直平分线MN交AC于D，下列四个结论正确的是