题目内容
15、如图，△ABC中AB=AC，∠A=36°，AB的垂直平分线MN交AC于D，下列四个结论正确的是①②③④
．（填序号）①△AMD≌△BMD；②AD=BD=BC；③△ABC∽△BDC； ④AD2=CD•AC．
分析：根据题意得∠ABC=∠C=72°，再由MN垂直平分AB，AD=AD，AM=BM，得△AMD≌△BMD，从而得出BD平分∠ABC，则∠CBD=36°，AD=BD=BC，即可得出△ABC∽△BDC，BC2=CD•AC．
解答：解：∵AB=AC，∠A=36°，
∴∠ABC=∠C=72°，
∵MN垂直平分AB，
∴AD=AD，AM=BM，
∴△AMD≌△BMD，故①正确；
∴∠A=∠ABD=36°，
∴∠CBD=36°，
∴BD=CD，
∴AD=BD=BC，故②正确；
∴△ABC∽△BDC，故③正确；
∴BC2=CD•AC．
即AD2=CD•AC，故④正确．
故答案为①②③④．
∴∠ABC=∠C=72°，
∵MN垂直平分AB，
∴AD=AD，AM=BM，
∴△AMD≌△BMD，故①正确；
∴∠A=∠ABD=36°，
∴∠CBD=36°，
∴BD=CD，
∴AD=BD=BC，故②正确；
∴△ABC∽△BDC，故③正确；
∴BC2=CD•AC．
即AD2=CD•AC，故④正确．
故答案为①②③④．
点评：本题考查了相似三角形的判定和性质、全等三角形的判定和性质、线段垂直平分线的性质以及等腰三角形的性质．
练习册系列答案
相关题目
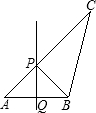如图，△ABC中AB的垂直平分线交AC、AB于点P、Q，若PC=2PA，AB=
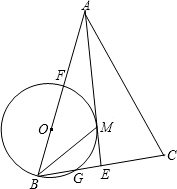交BC于G，交AB于点F，FB恰为⊙O的直径．
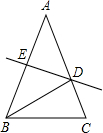如图，△ABC中AB=AC，AB的垂直平分线交AC于点D．若∠A=40°，则∠DBC=
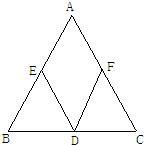15、如图，△ABC中AB=AC，EB=BD=DC=CF，∠A=40°，则∠EDF的度数是