��Ŀ����
����Ŀ����֪��![]() ��
��![]() ��
��![]() ��ͬһ��ֱ���ϣ�
��ͬһ��ֱ���ϣ�![]() ����һ�����ǰ��ֱ�Ƕ�����ڵ�
����һ�����ǰ��ֱ�Ƕ�����ڵ�![]() ����ͼ����ע��
����ͼ����ע��![]() ��
��![]() ��
��![]() ����
����
��1����ͼ1��ʹ���ǰ�Ķ�ֱ�DZ�![]() ������
������![]() �غϣ���
�غϣ���![]() __________��
__________��
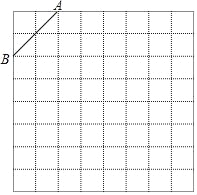
��2����ͼ2�������ǰ�![]() �Ƶ�
�Ƶ�![]() ��ʱ�뷽����ת����
��ʱ�뷽����ת����![]() ǡ��ƽ��
ǡ��ƽ��![]() ����˵��
����˵��![]() ����������
����������![]() ��ƽ���ߣ�
��ƽ���ߣ�
��3����ͼ3�������ǰ�![]() �Ƶ�
�Ƶ�![]() ��ʱ��ת����ʹ
��ʱ��ת����ʹ![]() ʱ����
ʱ����![]() �Ķ�����
�Ķ�����
��4����ͼ1�е����ǰ��Ƶ�![]() ��ÿ��5�����ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���
��ÿ��5�����ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���![]() ��ʱ��
��ʱ��![]() ǡ����ֱ��
ǡ����ֱ��![]() �غϣ���
�غϣ���![]() ��ֵ��
��ֵ��

���𰸡���1��![]() ����2��֤������������3��
����2��֤������������3��![]() ����4��28��64
����4��28��64
��������
��1����֪![]() ��
��![]() �����DOE=��COE+��BOC���������
�����DOE=��COE+��BOC���������![]() ������
������
��2��OEǡ��ƽ�֡�AOC���ɵá�AOE=��COE�����ݡ�DOE=90���á�AOE+��DOB=90������COE+��COD=90�����Ƴ���COD=��DOB�����ɵó��𰸣�
��3������ƽ�ǵ���180������֪![]() ��
��![]() ��
��![]() ���������BOD�Ķ�����
���������BOD�Ķ�����
��4���������������һ��֮�ڣ���OE������OC�ķ����ӳ����غ�ʱ�����ǰ��Ƶ�O��ת��140������OE������OC�غ�ʱ�����ǰ��Ƶ�O��ת��320���������г�������⼴�ɣ�
��1���ߡ�DOE=��COE+��BOC=![]() ��
��
�֡�![]() ��
��
���COE=![]() ��
��
��2����OEƽ�֡�AOC��
���COE=��AOE=![]() ��COA��
��COA��
�ߡ�EOD=![]() ��
��
���AOE+��DOB=![]() ����COE+��COD=
����COE+��COD=![]() ��
��
���COD=��DOB��
��OD���������ǡ�BOC��ƽ���ߣ�
��3�����COD=x�ȣ����AOE=4x�ȣ�
�ߡ�DOE=![]() ����BOC=
����BOC=![]() ��
��
��5x=40��
��x=8��
����COD=![]()
���BOD=![]()
��4����ͼ�������������
��һ��֮�ڣ���OE������OC�ķ����ӳ����غ�ʱ�����ǰ��Ƶ�O��ת��![]() ��
��
5t=140�� t=28��
��OE������OC�غ�ʱ�����ǰ��Ƶ�O��ת��![]() ��
��
5t=320��t=64��
���Ե�t=28���64��ʱ��OE��ֱ��OC�غϣ�
����������t��ֵΪ28��64��


 ��ѧ�����ϵ�д�
��ѧ�����ϵ�д� �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�