题目内容
【题目】阅读理解:
在平面直角坐标系中,任意两点![]() ,
,![]() 之间的位置关系有以下三种情形;
之间的位置关系有以下三种情形;
①如果![]() 轴,则
轴,则![]() ,
,![]()
②如果![]() 轴,则
轴,则![]() ,
,![]()
③如果![]() 与
与![]() 轴、
轴、![]() 轴均不平行,如图,过点
轴均不平行,如图,过点![]() 作与
作与![]() 轴的平行线与过点
轴的平行线与过点![]() 作与
作与![]() 轴的平行线相交于点
轴的平行线相交于点![]() ,则点
,则点![]() 坐标为
坐标为![]() ,由①得
,由①得![]() ;由②得
;由②得![]() ;根据勾股定理可得平面直角坐标系中任意两点的距离公式
;根据勾股定理可得平面直角坐标系中任意两点的距离公式![]()
小试牛刀:
(1)若点![]() 坐标为
坐标为![]() ,
,![]() 点坐标为
点坐标为![]() 则
则![]() ;
;
(2)若点![]() 坐标为
坐标为![]() ,
,![]() 点坐标为
点坐标为![]() 则
则![]() ;
;
(3)若点![]() 坐标为
坐标为![]() ,
,![]() 点坐标为
点坐标为![]() 则
则![]() ;
;
学以致用:
若点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 是
是![]() 轴上的动点,当
轴上的动点,当![]() 取得最小值时点
取得最小值时点![]() 的坐标为 并求出
的坐标为 并求出![]() 最小值=
最小值=
【答案】小试牛刀:(1)5;(2)6;(3)5;学以致用:![]() ,
,![]() .
.
【解析】
小试牛刀:(1)由于![]() 是平行于
是平行于![]() 轴,所以
轴,所以![]() ;
;
(2)此时![]() 是平行于
是平行于![]() 轴,所以
轴,所以![]() ;
;
(3)此时![]() 与
与![]() 轴、
轴、![]() 轴均不平行,按照题意,
轴均不平行,按照题意,![]() ,直接代入
,直接代入![]() 两点的坐标求解即可;
两点的坐标求解即可;
学以致用:根据两点之间线段最短可以得到,当![]() 三点共线时,
三点共线时,![]() 取得最小值,此时
取得最小值,此时![]() 点即为线段
点即为线段![]() 与
与![]() 轴的交点,所以可以解出直线
轴的交点,所以可以解出直线![]() 的解析式然后求一次函数与
的解析式然后求一次函数与![]() 轴的交点坐标,从而求出点
轴的交点坐标,从而求出点![]() 的坐标,而
的坐标,而![]() 的值即为线段
的值即为线段![]() 的值,可以根据题中给到的公式进行求解;
的值,可以根据题中给到的公式进行求解;
小试牛刀:(1)![]()
(2)![]()
(3)![]()
学以致用:∵点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,两点位于
,两点位于![]() 轴的异侧
轴的异侧
![]() 根据两点之间线段最短可得:当
根据两点之间线段最短可得:当![]() 三点共线时,
三点共线时,![]() 取得最小值,此时
取得最小值,此时![]() 点即为线段
点即为线段![]() 与
与![]() 轴的交点
轴的交点
设直线![]() 为
为![]()
则![]() ,解得
,解得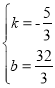 ,
,
∴直线![]() 为
为![]() ,令
,令![]() ,则
,则![]() ,即
,即![]() ,
,
此时![]() .
.
故答案是:![]() ,
,![]() .
.

练习册系列答案
相关题目