题目内容
【题目】某宾馆有50个房间供游客居住，当每个房间定价120元时，房间会全部住满，当每个房间每天的定价每增加10元时，就会有一个房间空闲，如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用，设每个房间定价为x元（x为整数）．
（1）直接写出每天游客居住的房间数量y与x的函数解析式．
（2）设宾馆每天的利润为W元，当每间房价定价为多少元时，宾馆每天所获利润最大，最大利润是多少？
【答案】（1）y＝﹣
x+62；（2）当每间房价定价为320元时，宾馆每天所获利润最大，最大利润是9000元．
【解析】
（1）根据每天游客居住的房间数量等于50﹣减少的房间数即可解决问题；
（2）构建二次函数，利用二次函数的性质解决问题．
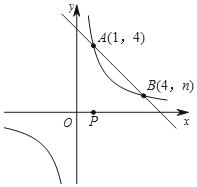
解：（1）y＝50﹣
＝﹣x+62；
（2）w＝（x﹣20）（﹣x+62）
＝﹣x2+64x﹣1240
＝﹣（x﹣320）2+9000，
∴当x＝320时，w取得最大值，最大值为9000，
答：当每间房价定价为320元时，宾馆每天所获利润最大，最大利润是9000元．
练习册系列答案
相关题目
【题目】某中学举行“校园朗读者”朗诵大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．
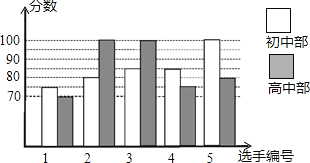
（1）根据图示填写表格；
平均分（分） | 中位数（分） | 众数（分） | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
（2）结合两队成绩的平均数和中位数， 队的决赛成绩较好；
（3）已知高中代表队决赛成绩的方差为160，计算初中代表队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定．（方差公式：S2＝
[（x1﹣
）2+（x2﹣）2+…+（xn﹣）2]
