题目内容
【题目】如图①,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A′的位置.通过计算我们知道:2∠A=∠1+∠2.请你继续探索:
(1)如果把△ABC纸片沿DE折叠,使点A落在四边形BCED外部点A′的位置,如图②所示.此时∠A与∠1、∠2之间存在什么样的关系?并说明理由.
(2)如果把四边形ABCD沿EF折叠,使点A、D分别落在四边形BCFE内部点A′、D′的位置,如图③所示.你能求出∠A′、∠D′、∠1 与∠2之间的关系吗?并说明理由.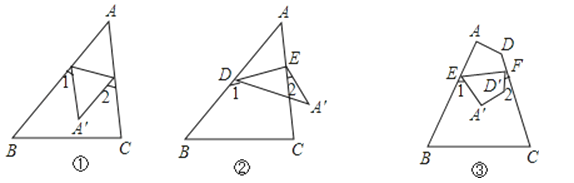
【答案】解:(1)连接AA′,
∵∠2=∠A′AE+∠AA′E,∠1=∠A′AD+∠AA′D;
∴∠1﹣∠2=2∠A;
(2)由图形折叠的性质可知∠1=180°﹣2∠AEF,∠2=180°﹣2∠DFE,
两式相加得,∠1+∠2=360°﹣2(∠AEF+∠DFE)
即∠1+∠2=360°﹣2(360°﹣∠A﹣∠D),
所以,∠1+∠2=2(∠A+∠D)﹣360°,
即:∠A+∠D=180°+![]() (∠1+∠2).
(∠1+∠2).
∴∠A′+∠D′=180°+![]() (∠1+∠2).
(∠1+∠2).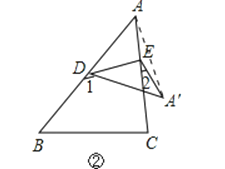
【解析】(1)连接AA′,根据三角形的外角的性质以及轴对称的性质进行分析;
(2)根据平角的定义以及四边形的内角和定理进行探讨即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目