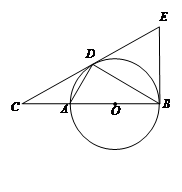题目内容
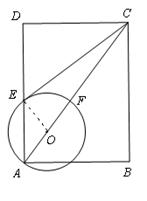
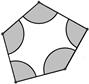
如图,在矩形ABCD中,点O在对角线AC上,以OA长为半径的 与AD,AC分别交于点E,F,∠ACB="∠DCE" .
与AD,AC分别交于点E,F,∠ACB="∠DCE" .
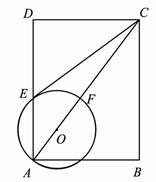
小题1:请判断直线CE与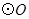 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
小题2:若 DE:EC=1: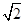 ,
, 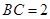 ,求⊙O的半径.
,求⊙O的半径.
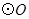 与AD,AC分别交于点E,F,∠ACB="∠DCE" .
与AD,AC分别交于点E,F,∠ACB="∠DCE" .
小题1:请判断直线CE与
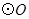 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;小题2:若 DE:EC=1:
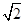 ,
, 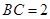 ,求⊙O的半径.
,求⊙O的半径.小题1:直线CE与
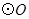 相切
相切证明:∵矩形ABCD ,
∴BC//AD,∠ACB=∠DAC.
∵
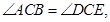
∴
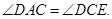
连接OE,则
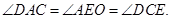
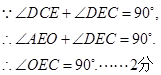
∴直线CE与
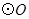 相切
相切小题1:








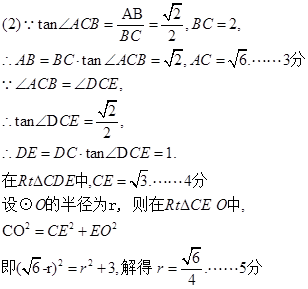
小题1:首先连接OE,由OE=OA与四边形ABCD是矩形,易求得∠DEC+∠OEA=90°,即OE⊥EC,即可证得直线CE与⊙O的位置关系是相切;
小题1:首先易证得△CDE∽△CBA,然后根据相似三角形的对应边成比例,即可求得DE的长,又由勾股定理即可求得AC的长,然后设OA为x,即可得方程(
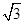 )2+x2=(
)2+x2=(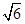 -x)2,解此方程即可求得⊙O的半径.
-x)2,解此方程即可求得⊙O的半径.
练习册系列答案
相关题目
 .
.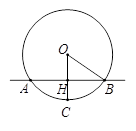
 是
是 的直径,点
的直径,点 在
在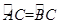 .动点
.动点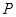 在弦
在弦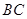 上,则
上,则 可能为_________度(写出一个符合条件的度数即可).
可能为_________度(写出一个符合条件的度数即可).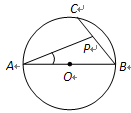
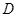 为
为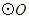 上一点,点
上一点,点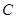 在直径
在直径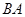 的延长线上,
的延长线上,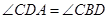 .
.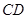 是
是 作
作 ,若
,若 ,求
,求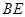 的长.
的长.