题目内容
在等腰△ABC中，AB=AC，D是AC上一点，且AD=BD=BC，则∠BDC的度数为
- A.36°
- B.72°
- C.108°
- D.60°
B
分析：由已知条件开始，通过线段相等，得到角相等，再由三角形内角和求出各个角的大小．
解答：∵AB=AC，∴∠C=∠ABC，
∵AD=BD=BC，∴∠A=∠ABD，∠C=∠BDC=2∠A，
∵三角形内角和为180°
∴∠A=36°
∠BDC=2∠A=72°
故选B．
点评：本题考查了等腰三角形的性质；熟练掌握等于三角形的性质，以及三角形内角和定理，得到各角之间的关系式解答本题的关键．
分析：由已知条件开始，通过线段相等，得到角相等，再由三角形内角和求出各个角的大小．
解答：∵AB=AC，∴∠C=∠ABC，
∵AD=BD=BC，∴∠A=∠ABD，∠C=∠BDC=2∠A，
∵三角形内角和为180°
∴∠A=36°
∠BDC=2∠A=72°
故选B．
点评：本题考查了等腰三角形的性质；熟练掌握等于三角形的性质，以及三角形内角和定理，得到各角之间的关系式解答本题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
8、如图所示，在等腰△ABC中，点D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为E、F，图中有几对全等三角形（ ）
（2013•闸北区二模）如图，在等腰△ABC中，底边BC的中点是点D，底角的正切值是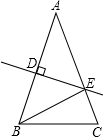
如图，在等腰△ABC中，AB=AC=10cm，直线DE垂直平分AB，分别交AB、AC于D、E两点．若BC=8cm，则△BCE的周长是
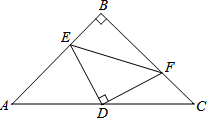如图，在等腰△ABC中，∠ABC=90°，D为底边AC中点，过D点作DE⊥DF，交AB于E，交BC于F．若AE=12，FC=5，