题目内容
在等腰△ABC中，AB=AC，∠A=80°，则一腰上的高CD与底边BC的夹角为（ ）
分析：先根据三角形内角和定理及等边对等角的性质求出∠C=50°，然后在直角△DBC中，利用直角三角形两锐角互余即可求解．
解答：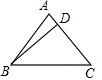
解：如图，∵在等腰△ABC中，AB=AC，∠A=80°，
∴∠C=∠ABC=
=50°，
在直角△DBC中，
∵∠BDC=90°，
∴∠DBC=90°-50°=40°．
故选B．
解：如图，∵在等腰△ABC中，AB=AC，∠A=80°，∴∠C=∠ABC=
| 180°-80° |
| 2 |
在直角△DBC中，
∵∠BDC=90°，
∴∠DBC=90°-50°=40°．
故选B．
点评：本题主要考查了等腰三角形的性质与三角形内角和定理及其推论，是基础知识，难度适中．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8、如图所示，在等腰△ABC中，点D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为E、F，图中有几对全等三角形（ ）
（2013•闸北区二模）如图，在等腰△ABC中，底边BC的中点是点D，底角的正切值是
如图，在等腰△ABC中，AB=AC=10cm，直线DE垂直平分AB，分别交AB、AC于D、E两点．若BC=8cm，则△BCE的周长是
如图，在等腰△ABC中，∠ABC=90°，D为底边AC中点，过D点作DE⊥DF，交AB于E，交BC于F．若AE=12，FC=5，