题目内容
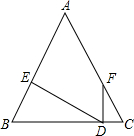 如图,△ABC,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,那么∠FDE的度数为
如图,△ABC,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,那么∠FDE的度数为
- A.68°
- B.60°
- C.120°
- D.58°
A
分析:先根据等角的余角相等得出∠EDB=∠CFD,再由邻补角定义求出∠CFD即∠EDB的数,从而可求得∠EDF的度数.
解答: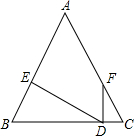 解:∵FD⊥BC于D,DE⊥AB于E,
解:∵FD⊥BC于D,DE⊥AB于E,
∴∠BED=∠FDC=90°,
∵∠B=∠C,
∴∠EDB=∠CFD,
∵∠AFD=158°,
∴∠EDB=∠CFD=180°-158°=22°,
∴∠EDF=90°-∠EDB=90°-22°=68°.
故选A.
点评:本题主要考查垂线的定义、余角的性质、邻补角的定义等知识,比较简单.
分析:先根据等角的余角相等得出∠EDB=∠CFD,再由邻补角定义求出∠CFD即∠EDB的数,从而可求得∠EDF的度数.
解答:
 解:∵FD⊥BC于D,DE⊥AB于E,
解:∵FD⊥BC于D,DE⊥AB于E,∴∠BED=∠FDC=90°,
∵∠B=∠C,
∴∠EDB=∠CFD,
∵∠AFD=158°,
∴∠EDB=∠CFD=180°-158°=22°,
∴∠EDF=90°-∠EDB=90°-22°=68°.
故选A.
点评:本题主要考查垂线的定义、余角的性质、邻补角的定义等知识,比较简单.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
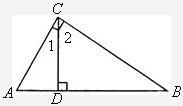
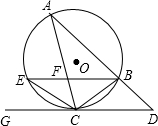 ,且CB=CE.
,且CB=CE.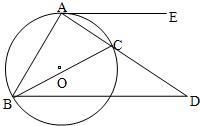 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.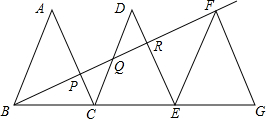 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且