题目内容
如图，Rt△ABC中，∠C=90°，∠A=30°，AC=2cm，求直角边BC的长．
解：∵∠C=90°，∠A=30°，
∴BC=
AB，
∵AB2=AC2+BC2，AC=2cm，
∴（2BC）2=4+BC2，解得BC=±
，
∵BC＞0，
∴BC=，即直角边BC的长为．
分析：先根据直角三角形的性质得出BC=AB，再根据勾股定理可得到AB2=AC2+BC2，把AC=2cm，BC=AB代入即可求出BC的长．
点评：本题考查的是勾股定理及含30度角的直角三角形的特点，根据勾股定理得出直角三角形三边之间的数量关系式解答此题的关键．
∴BC=
AB，∵AB2=AC2+BC2，AC=2cm，
∴（2BC）2=4+BC2，解得BC=±
，∵BC＞0，
∴BC=
，即直角边BC的长为．分析：先根据直角三角形的性质得出BC=
AB，再根据勾股定理可得到AB2=AC2+BC2，把AC=2cm，BC=AB代入即可求出BC的长．点评：本题考查的是勾股定理及含30度角的直角三角形的特点，根据勾股定理得出直角三角形三边之间的数量关系式解答此题的关键．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
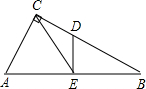如图，Rt△ABC中，∠ACB=90°，tanB=
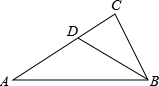如图，Rt△ABC中，∠C=90°，BC=3，AC=4，若△ABC∽△BDC，则CD=（ ）
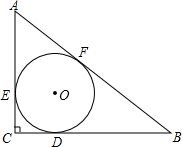如图，Rt△ABC中，∠C=90°，△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F．
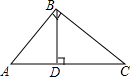如图，Rt△ABC中，∠ABC=90゜，BD⊥AC于D，∠CBD=α，AB=3，BC=4．