题目内容
【题目】完成下列证明过程. 如图,在△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B,说明ED=EF.
解:∵∠DEC=∠B+∠BDE (),
又∵∠DEF=∠B(已知),
∴∠=∠(等式性质).
在△EBD与△FCE中,
∠=∠(已证),
=(已知),
∠B=∠C(已知),
∴△EBD≌△FCE().
∴ED=EF ().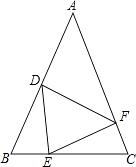
【答案】三角形外角的性质;BDE;CEF;BDE;CEF;BD;CE;ASA;全等三角形的对应边相等
【解析】解: ∵∠DEC=∠B+∠BDE (三角形外角的性质),
又∵∠DEF=∠B(已知),
∴∠BDE=∠CEF(等式性质).
在△EBD与△FCE中,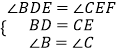
∴△EBD≌△FCE(ASA).
∴ED=EF (全等三角形的对应边相等).
所以答案是:三角形外角的性质;BDE;CEF;BDE;CEF;BD;CE;ASA;全等三角形的对应边相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某班级进行了一次诗歌朗诵比赛,甲、乙两组学生的成绩如表所示:
组别 | 平均分 | 中位数 | 方差 |
甲 | 6.9 | 8 | 2.65 |
乙 | 7.1 | 7 | 0.38 |
你认为哪一组的成绩更好一些?并说明理由.
答:组(填“甲”或“乙”),理由是 .