Question

【题目】平面直角坐标系中，抛物线y=ax2+bx+2过点A（﹣3，0）、B （1，0），与y轴交于点C，抛物线的顶点为D，点G在抛物线上且其纵坐标为2．
（1）a= ， b= ， D（ ， ）．
（2）P是线段AB上一动点（点P不与A、B重合），点P作x轴的垂线交抛物线于点E．
①若PE=PB，试求E点坐标；
②在①的条件下，PE、DG交于点M，在线段PE上是否存一点N，使得△DMN与△DCO相似？若存在，试求出相应点的坐标；
③在①的条件下，点F是坐标轴上一点，且点F到EC、ED的距离相等，试直接写出EF的长度．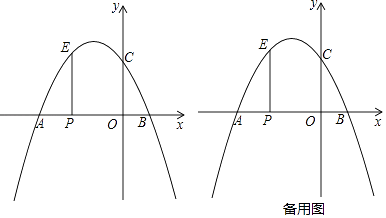

Answer 1

【答案】
（1）﹣ ；﹣ ；﹣1；
（2）

①设P（x，0），则E（x，﹣ x2﹣ x+2），则PB=1﹣x，PE=﹣ x2﹣ x+2．

∵PE=PB，

∴﹣ x2﹣ x+2=1﹣x．

∴x1=1（舍去），x2=﹣ ．

当x=﹣ ，函数值y= ．

∴E（﹣ ， ）．

②存在点N（﹣ ， ），理由如下：过点G作GH⊥x轴，垂足为H，连结DH．

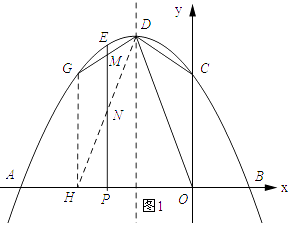
把y=2代入抛物线的解析式得：2=﹣ x2﹣ x+2，解得x=0或x=﹣2．

∴G（﹣2，2）．

抛物线的对称轴为x=﹣1，

∵GH⊥x轴，

∴H（﹣2，0）．

∴△DOC与△DHG关于直线x=﹣1对称．

∴要使DMN与△DCO相似，只需△DMN与△DGH相似．

∵MN∥GH，

∴△DMN∽△DGH．

设直线DH的解析式为y=kx+b，将点H和点D的坐标代入得： ，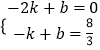

解得：k= ，b= ．

∴直线DH的解析式为y= x+ ．

将x=﹣ 代入得：y= ．

∴N（﹣ ， ）．

③如图2所示：过点E作EF⊥y轴，交抛物线的对称轴与点G，则G（﹣1， ）过点E作EF′⊥x垂足为F′．

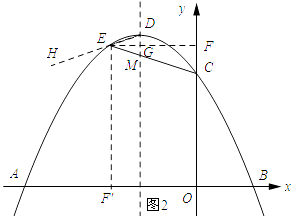
设直线EC的解析式为y=mx+n将点E和点C的坐标代入得： ，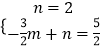

解得：m=﹣ ，n=2．

∴直线EC的解析式为y= x+2．

当x=﹣1时，y= ．

∴DG=GM．

∴点M与点D关于EF对称．

∴EF是∠DEC的角平分线．

∴点F到点F到EC、ED的距离相等．

∴EF= ．

∵EF′⊥x垂足为F′．

∴∠FEF′=90°，

∴∠DEF+∠HEF′=90°，∠FEC+∠CEF′=90°．

又∵∠DEF=∠FEC，

∴∠HEF′=∠CEF′．

∴EF′是∠HEC的平分线，

∴点F′到DE和EC的距离相等．

∴EF′= ．

综上所述，EF的长为 或 ．

【解析】解：（1）把x=0代入抛物线的解析式得：y=2，
∴C（0，2）．
设抛物线的解析式为y=a（x+3）（x﹣1），将点C的坐标代入得﹣3a=2，解得：a=﹣ ．
∴抛物线的解析式为y=﹣ （x+3）（x﹣1）=﹣ x2﹣ x+2．
∴b=﹣ ．
∴x=﹣ =﹣1．
当x=﹣1时，y= ．
∴D（﹣1， ）．
所以答案是：﹣ ；﹣ ；﹣1， ．