ћвƒњƒЏ»Ё
 “—÷™°—Oµƒ÷±ЊґAB=10£ђ”–“їґѓµгCі”Aµг—Ў‘≤÷№Ћ≥ ±’лѕтµгB‘Ћґѓ£ђ»фµгDќ™ѕ“ACЋщґ‘ї°µƒ»эµ»Ј÷µг£ђєэµгD„чDE°ЌAB”ЏE£ђ÷±ѕяACљї÷±ѕяDB”ЏG£ђµгC°ҐDґЉ≤ї”л÷±ЊґABЅљґЋµг÷ЎЇѕ£ђ
“—÷™°—Oµƒ÷±ЊґAB=10£ђ”–“їґѓµгCі”Aµг—Ў‘≤÷№Ћ≥ ±’лѕтµгB‘Ћґѓ£ђ»фµгDќ™ѕ“ACЋщґ‘ї°µƒ»эµ»Ј÷µг£ђєэµгD„чDE°ЌAB”ЏE£ђ÷±ѕяACљї÷±ѕяDB”ЏG£ђµгC°ҐDґЉ≤ї”л÷±ЊґABЅљґЋµг÷ЎЇѕ£ђ£®1£©»зЌЉ£ђ»ф
 |
| AD |
| 1 |
| 3 |
 |
| ADC |
£®2£©‘ЏµгCµƒ‘Ћґѓєэ≥ћ÷– «Јсіж‘Џ“‘G°ҐC°ҐBќ™ґ•µгµƒ»эљ«–ќЇЌ°чABCѕаЋ∆£њ»ф”–«лї≠≥цѕа”¶„іћђЌЉ£ђ≤Ґ«у≥цѕа”¶ѕяґќEBµƒ≥§£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
Ј÷ќц£Ї£®1£©ҐўЅђљ”OD£ђ”…
=
=45°гµ√µљ°ѕAOD=45°г£ђ»їЇуЄщЊЁї°≥§єЂ љЉ∆Ћгї°ADµƒ≥§ґ»£ї
ҐЏ”…DE°ЌAB£ђ“„µ√°чODEќ™µ»—ь÷±љ«»эљ«–ќ£ђ»їЇуЄщЊЁµ»—ь÷±љ«»эљ«–ќµƒ–‘÷ њ…µ√µљDE=
OD=
£ї
Ґџ‘ЏRt°чBDE÷–£ђЄщЊЁєіє…ґ®јнЉ∆Ћг≥цDE=
=5
£ђ”…ABќ™°—Oµƒ÷±Њґ£ђЄщЊЁ‘≤÷№љ«ґ®јнµ√°ѕC=90°г£ђ“„ї°BCµƒґ» э «45°г£ђї°CDµƒґ» э «90°г£ђ‘т°ѕCBD=45°г£ђ‘т°чCBGќ™µ»—ь÷±љ«»эљ«–ќ£їљ”„≈÷§√чRt°чABC°„Rt°чBDE£ђјы”√ѕаЋ∆Љ∆Ћг≥цBC=
£ђ»їЇуЄщЊЁ°чBCGµƒ√жїэ=
BC2љш––Љ∆Ћг£ї
£®2£©µ±ї°DC=ї°BC ±£ђ°ѕBAC=°ѕDBC£ђЉіњ…µ√µљRt°чCBG°„Rt°чCAB£ї”…µгDќ™ѕ“ACЋщґ‘ї°µƒ»эµ»Ј÷µг£ђ‘т°ѕBAC=°ѕDBC=2°ѕABD£ђ“„µ√°ѕABD=18°г£ђЅђљ”AD£ђЄщЊЁABќ™÷±Њґµ√µљ°ѕADB=90°г£ђ‘ЏRt°чABD÷–£ђAB=10£ђ°ѕABD=18°г£ђЄщЊЁ”аѕ“µƒґ®“еµ√BD=10cos18°г£ђ‘ЏRt°чDEB÷–£ђЄщЊЁ’эѕ“µƒґ®“еµ√DE=BDsin18°г£ђЋщ“‘DE=10cos18°г•sin18°г£Ѓ
 |
| AD |
| 1 |
| 3 |
 |
| ADC |
ҐЏ”…DE°ЌAB£ђ“„µ√°чODEќ™µ»—ь÷±љ«»эљ«–ќ£ђ»їЇуЄщЊЁµ»—ь÷±љ«»эљ«–ќµƒ–‘÷ њ…µ√µљDE=
| ||
| 2 |
5
| ||
| 2 |
Ґџ‘ЏRt°чBDE÷–£ђЄщЊЁєіє…ґ®јнЉ∆Ћг≥цDE=
| DE2+BE2 |
2+
|
5
| ||||
|
| 1 |
| 2 |
£®2£©µ±ї°DC=ї°BC ±£ђ°ѕBAC=°ѕDBC£ђЉіњ…µ√µљRt°чCBG°„Rt°чCAB£ї”…µгDќ™ѕ“ACЋщґ‘ї°µƒ»эµ»Ј÷µг£ђ‘т°ѕBAC=°ѕDBC=2°ѕABD£ђ“„µ√°ѕABD=18°г£ђЅђљ”AD£ђЄщЊЁABќ™÷±Њґµ√µљ°ѕADB=90°г£ђ‘ЏRt°чABD÷–£ђAB=10£ђ°ѕABD=18°г£ђЄщЊЁ”аѕ“µƒґ®“еµ√BD=10cos18°г£ђ‘ЏRt°чDEB÷–£ђЄщЊЁ’эѕ“µƒґ®“еµ√DE=BDsin18°г£ђЋщ“‘DE=10cos18°г•sin18°г£Ѓ
љвір£Їљв£Ї£®1£©ҐўЅђљ”OD£ђ»зЌЉ£ђ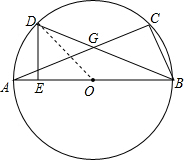
°я
=
=45°г£ђ
°а°ѕAOD=45°г£ђ
°яAB=10£ђ
°аOA=OD=5£ђ
°аї°ADµƒ≥§ґ»=
=
¶–£ї
ҐЏ°яDE°ЌAB£ђ
°а°ѕDEO=90°г£ђ
°я°ѕDOA=45°г£ђ
°а°чODEќ™µ»—ь÷±љ«»эљ«–ќ£ђ
°аDE=
OD=
°Ѕ5=
£ї
Ґџ‘ЏRt°чBDE÷–£ђDE=
£ђBE=OB+OE=5+
£ђ
°аDE=
=5
£ђ
°яABќ™°—Oµƒ÷±Њґ£ђ
°а°ѕC=90°г£ђ
°я
=
=45°г£ђ
°аї°BCµƒґ» э «180°г-45°г°Ѕ3=45°г£ђї°CDµƒґ» э «2°Ѕ45°г=90°г£ђ
°а°ѕCBD=45°г£ђ
°а°ѕCGB=°ѕB=45°г£ђ
°а°чCBGќ™µ»—ь÷±љ«»эљ«–ќ£ї
°я
ЇЌ
µƒґ» эґЉќ™45°г£ђ
°а°ѕABD=°ѕBAC£ђ
°аRt°чABC°„Rt°чBDE£ђ
°а
=
£ђЉі
=
£ђ
°аBC=
£ђ
°а°чBCGµƒ√жїэ=
BC2=
°Ѕ£®
£©2=
£ї
£®2£©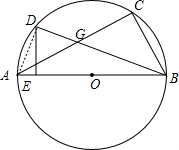 іж‘Џ£Ѓ
іж‘Џ£Ѓ
µ±ї°DC=ї°BC ±£ђ°ѕBAC=°ѕDBC£ђ
°аRt°чCBG°„Rt°чCAB£ђ
°яµгDќ™ѕ“ACЋщґ‘ї°µƒ»эµ»Ј÷µг£ђ
°а°ѕBAC=°ѕDBC=2°ѕABD£ђ
…и°ѕABD=¶Ѕ£ђ‘т°ѕBAC=°ѕDBC=2¶Ѕ£ђ
°а¶Ѕ+2¶Ѕ+2¶Ѕ=90°г£ђљвµ√¶Ѕ=18°г£ђ
°а°ѕABD=18°г£ђ
Ѕђљ”AD£ђ
°яABќ™÷±Њґ£ђ
°а°ѕADB=90°г£ђ
‘ЏRt°чABD÷–£ђAB=10£ђ°ѕABD=18°г£ђ
°аBD=10cos18°г£ђ
‘ЏRt°чDEB÷–£ђDE=BDsin18°г£ђ
°аDE=10cos18°г•sin18°г£Ѓ

°я
 |
| AD |
| 1 |
| 3 |
 |
| ADC |
°а°ѕAOD=45°г£ђ
°яAB=10£ђ
°аOA=OD=5£ђ
°аї°ADµƒ≥§ґ»=
| 45¶–•5 |
| 180 |
| 5 |
| 4 |
ҐЏ°яDE°ЌAB£ђ
°а°ѕDEO=90°г£ђ
°я°ѕDOA=45°г£ђ
°а°чODEќ™µ»—ь÷±љ«»эљ«–ќ£ђ
°аDE=
| ||
| 2 |
| ||
| 2 |
5
| ||
| 2 |
Ґџ‘ЏRt°чBDE÷–£ђDE=
5
| ||
| 2 |
5
| ||
| 2 |
°аDE=
| DE2+BE2 |
2+
|
°яABќ™°—Oµƒ÷±Њґ£ђ
°а°ѕC=90°г£ђ
°я
 |
| AD |
| 1 |
| 3 |
 |
| ADC |
°аї°BCµƒґ» э «180°г-45°г°Ѕ3=45°г£ђї°CDµƒґ» э «2°Ѕ45°г=90°г£ђ
°а°ѕCBD=45°г£ђ
°а°ѕCGB=°ѕB=45°г£ђ
°а°чCBGќ™µ»—ь÷±љ«»эљ«–ќ£ї
°я
 |
| AD |
 |
| BC |
°а°ѕABD=°ѕBAC£ђ
°аRt°чABC°„Rt°чBDE£ђ
°а
| BC |
| DE |
| AB |
| DE |
| BC | ||||
|
| 10 | ||||
5
|
°аBC=
5
| ||||
|
°а°чBCGµƒ√жїэ=
| 1 |
| 2 |
| 1 |
| 2 |
5
| ||||
|
50-25
| ||
| 2 |
£®2£©
 іж‘Џ£Ѓ
іж‘Џ£Ѓµ±ї°DC=ї°BC ±£ђ°ѕBAC=°ѕDBC£ђ
°аRt°чCBG°„Rt°чCAB£ђ
°яµгDќ™ѕ“ACЋщґ‘ї°µƒ»эµ»Ј÷µг£ђ
°а°ѕBAC=°ѕDBC=2°ѕABD£ђ
…и°ѕABD=¶Ѕ£ђ‘т°ѕBAC=°ѕDBC=2¶Ѕ£ђ
°а¶Ѕ+2¶Ѕ+2¶Ѕ=90°г£ђљвµ√¶Ѕ=18°г£ђ
°а°ѕABD=18°г£ђ
Ѕђљ”AD£ђ
°яABќ™÷±Њґ£ђ
°а°ѕADB=90°г£ђ
‘ЏRt°чABD÷–£ђAB=10£ђ°ѕABD=18°г£ђ
°аBD=10cos18°г£ђ
‘ЏRt°чDEB÷–£ђDE=BDsin18°г£ђ
°аDE=10cos18°г•sin18°г£Ѓ
µг∆ј£Ї±ЊћвњЉ≤йЅЋ‘≤µƒ„џЇѕћв£Ї мЅЈ’∆ќ’‘≤÷№љ«ґ®јнЉ∞∆дЌ∆¬џ°Ґµ»—ь÷±љ«»эљ«–ќµƒ≈–ґ®”л–‘÷ £їїб‘Ћ”√ѕаЋ∆±»°Ґєіє…ґ®јнЇЌ»сљ«»эљ«–ќЇѓ эµƒґ®“ељш––ЉЄЇќЉ∆Ћг£Ѓ

ЅЈѕ∞≤бѕµЅ–ір∞Є
ѕаєЎћвƒњ
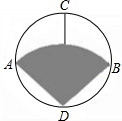 ƒ≥÷÷…ћ∆Јµƒ…ћ±кЌЉ∞Є»зЌЉ£®ЌЉ÷–µƒ“х”∞≤њЈ÷£©£ђ“—÷™°—Oµƒ÷±ЊґAB°ЌCD£ђ«“AB=8cm£ђї°AB «“‘Dќ™‘≤–ƒ£ђDAќ™∞лЊґµƒї°£ђ‘т…ћ±кЌЉ∞Єµƒ√жїэќ™
ƒ≥÷÷…ћ∆Јµƒ…ћ±кЌЉ∞Є»зЌЉ£®ЌЉ÷–µƒ“х”∞≤њЈ÷£©£ђ“—÷™°—Oµƒ÷±ЊґAB°ЌCD£ђ«“AB=8cm£ђї°AB «“‘Dќ™‘≤–ƒ£ђDAќ™∞лЊґµƒї°£ђ‘т…ћ±кЌЉ∞Єµƒ√жїэќ™ »зЌЉ£ђ“—÷™°—Oµƒ÷±ЊґAB”лѕ“CDї•ѕаіє÷±£ђіє„гќ™µгE£Ѓ°—Oµƒ«–ѕяBF”лѕ“ACµƒ—”≥§ѕяѕаљї”ЏµгF£ђ«“AC=8£ђtan°ѕBDC=
»зЌЉ£ђ“—÷™°—Oµƒ÷±ЊґAB”лѕ“CDї•ѕаіє÷±£ђіє„гќ™µгE£Ѓ°—Oµƒ«–ѕяBF”лѕ“ACµƒ—”≥§ѕяѕаљї”ЏµгF£ђ«“AC=8£ђtan°ѕBDC=