题目内容
（2011•营口）已知⊙O的直径AB=2，过点A的两条弦AC=
，AD=
，则∠CBD=
| 2 |
| 3 |
15°或105°（只答对一个给1分）
15°或105°（只答对一个给1分）
．分析：分两条弦在直径AB的同侧和异侧两种情况讨论即可求解．
解答：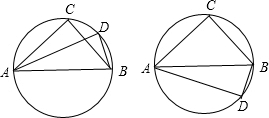
解：∵AB为⊙O的直径，
∴∠ACB=∠ADB=90°．
在△ABC中，∵∠ACB=90°，AB=2，AC=
，
∴sin∠ABC=
=
，∴∠ABC=45°；
在△ABD中，∵∠ADB=90°，AB=2，AD=
，
∴sin∠ABD=
=
，∴∠ABD=60°．
分两种情况：
①当两条弦AC与AD在直径AB的同侧时，∠CBD=∠ABD-∠ABC=15°；
②当两条弦AC与AD在直径AB的异侧时，∠CBD=∠ABD+∠ABC=105°．
综上可知∠CBD=15°或105°．
故答案为15°或105°．
解：∵AB为⊙O的直径，∴∠ACB=∠ADB=90°．
在△ABC中，∵∠ACB=90°，AB=2，AC=
| 2 |
∴sin∠ABC=
| AC |
| AB |
| ||
| 2 |
在△ABD中，∵∠ADB=90°，AB=2，AD=
| 3 |
∴sin∠ABD=
| AD |
| AB |
| ||
| 2 |
分两种情况：
①当两条弦AC与AD在直径AB的同侧时，∠CBD=∠ABD-∠ABC=15°；
②当两条弦AC与AD在直径AB的异侧时，∠CBD=∠ABD+∠ABC=105°．
综上可知∠CBD=15°或105°．
故答案为15°或105°．
点评：本题考查了解直角三角形及圆周角定理，难度中等，能够考虑到两条弦AC、AD与直径AB的位置关系，从而进行分类讨论是解决本题的关键．
练习册系列答案
相关题目
（2011•营口）如图，已知AB是⊙O的直径，PB为⊙O的切线，B为切点，OP⊥弦BC于点D且交⊙O于点E．